尽管二进制搜索树 (BST) 被广泛使用,但随着数据的添加,二进制搜索树往往会随着时间的推移退化为无序的链接列表。”红黑树”是一种相关的二进制树类型,通常更适合某些类型的搜索操作。本文讨论了红黑树如何促进更快的搜索速度,并随着时间的推移变得不像类似的数据结构,并演示如何在 C# 中构建和搜索红黑树。
树是一种数据结构,通过将分层数据存储在以特定方式相互相关的节点中来表示分层数据。树的最顶端节点称为根。它是树的所有其他节点从该节点下降的节点。树可以只有一个根。使用相同的逻辑,树应至少具有一个节点 -根节点。BST 是一种特殊的树结构,可确保树节点进行排序,并且每个节点都包含一个值。在二进制树中,每个节点可能只有两个子节点,称为左节点和右内部节点。对于任何给定节点,左侧子节点存储的值小于当前节点的值,而右子节点的值大于当前节点的值。此类树具有”高度”,您可以通过计算从根节点到树中最深层节点(离根最远的节点)的链接数来计算。
图 1 中的树有 9 个节点,高度为 3 个节点,即从根节点 (8) 到任何节点 4、7 或 13 的距离。请注意,当右节点存储的值大于其父节点时,所有左节点的值都小于其父节点。没有子节点的节点称为”叶节点”。在图 1 中,对应于值 1、4、7 和 13 的节点都是叶节点。
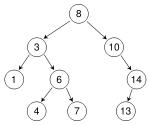
要搜索二进制树中的特定项,请从根节点开始,并反复获取左分支或右分支,具体取决于要搜索的值是否大于或小于当前节点的值。二进制树中的搜索操作采用 O(h) 时间单位,其中 h 表示树的高度。当添加的节点不成比例地落入树的一个分支中时,BST 很容易退化为不平衡列表,从而使该分支的搜索时间比其他分支长得多。如果按顺序或接近顺序插入插入到 BST 中的项目,则会发生这种情况。在这种情况下,BST 的性能不会比数组更好。这是红黑树木适合图片的地方。
红黑树是 BST 的优化版本,它为每个节点添加颜色属性。此颜色属性值的值始终为红色或黑色。根节点始终为黑色。除了颜色之外,每个节点还包含对其父节点及其子节点(左节点和右节点)的引用,以及可选的键值。红黑树的性能优于普通 BST,因为它们使用颜色属性和节点引用来保持更好的平衡。
红黑树总是遵循以下规则:
- 红黑树的根节点始终为黑色。
- 从树根到任何叶节点的路径包含整个树中相同数量的黑色节点,也称为树的”黑色高度”。
- 红色节点的两个子节点始终为黑色。
- 所有”外部”节点(叶节点)始终呈黑色。
包含 n 节点的红黑树的最大高度由 2log(n+1)给出。在红黑树中搜索任何项目所采用的时间遵循公式 O(log n),这意味着它是搜索操作的最佳选择。图 2 显示了典型的红黑树。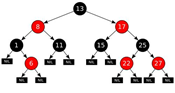
在 C 中实现 BST#
首先查看二进制搜索树的代码是值得的;您可以使用它查看红黑树实现有何不同,并用于比较测试。清单1中的代码实现了一个简单的二进制搜索树。查看用于搜索树的递归代码很有趣:
xxxxxxx
公共节点搜索(节点节点对象键)
{
如果(节点=空)
返回null;
还
11
{
12
13
int结果=字符串。比较(键.到 String(),
14
15
节点.键。到弦());
16
17
19
如果(结果<0)
20
21
返回搜索(节点)。左键;
22
23
否则如果(结果>0)
24
25
右,键);
26
27
否则
28
29
返回节点;
30
31
}
32
33
搜索方法比较键参数的字符串值和传入节点的键。当键值小于(搜索左侧子值)或大于节点参数的键值(搜索右侧子值)时,该比较的结果将设置递归调用以搜索。当搜索向下树进行时,最终键值将与节点值匹配,从而导致搜索成功,或者搜索将失败,该方法将返回 null。
在 C 中实现红黑树#
本文的其余部分讨论了红黑树实现,演示如何使用它来搜索数据,并演示了比较搜索操作在红黑树和二进制树实现之间的大型数据集的效率的示例。
首先创建一个包含两个表示红黑树节点颜色的整数常数的枚举:
Java
xxxxxxx
1
公共枚举颜色
2
3
{
4
5
红色=0黑色=1
6
7
}
您还需要一个包含方向的枚举,该等数由称为"左"和"右"的常量表示:
Java
