Posted by on | Featured

在 “为什么使用 K 表示时间序列数据？(第一部分), “我给出了如何使用不同的统计函数和 k-均值聚类进行时间序列数据异常检测的概述。如果你不熟悉, 我建议你检查一下。在这篇文章中, 我将分享:

  1. 一些代码, 显示如何使用 K 手段。
  2. 为什么不应该使用 K 手段进行上下文时间序列异常检测。

一些代码显示它是如何使用的

我借用了这部分的代码和数据集, 从鱼的教程。请看一下, 很棒。在本例中, 我将向您展示如何通过 K 表示聚类的上下文异常检测来检测心电图数据中的异常。节律性心电图数据的断裂是一类集体异常, 但我们将分析数据的形状 (或上下文) 的异常。

用 k-均值法检测心电图数据异常的方法

K 意味着会形成集群。但如何？时间序列数据看起来不像一个美丽的散布情节, 是 “群集”。对数据进行窗口化会获取类似于此的数据.。

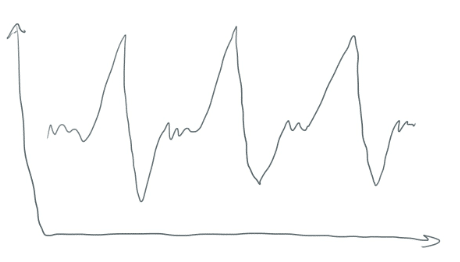
把它变成一堆较小的片段 (每个都有32分)。它们本质上是横向的翻译。他们看起来像这样..。

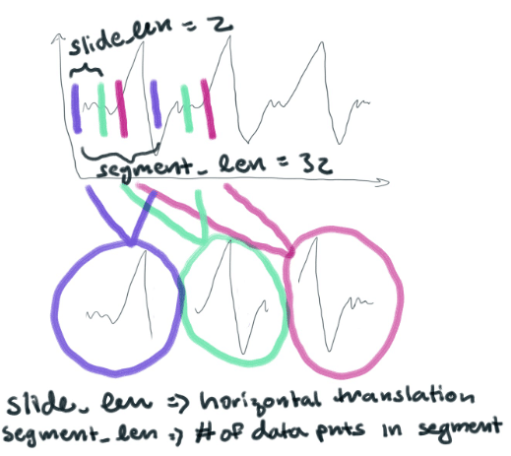
Image title

每个窗口段都由一个大小为32的数组定义。

然后, 我们将在每个线段中的每个点, 并在32维空间中绘制它。我喜欢把3维以上的东西看成是一朵模糊不清的云彩。你可以想象, 我们现在正在一个更大的空间中绘制一堆32维的云。K 意味着将这些32维的云聚集在一起, 根据它们彼此的相似程度。这样, 群集将表示数据所采用的不同形状。

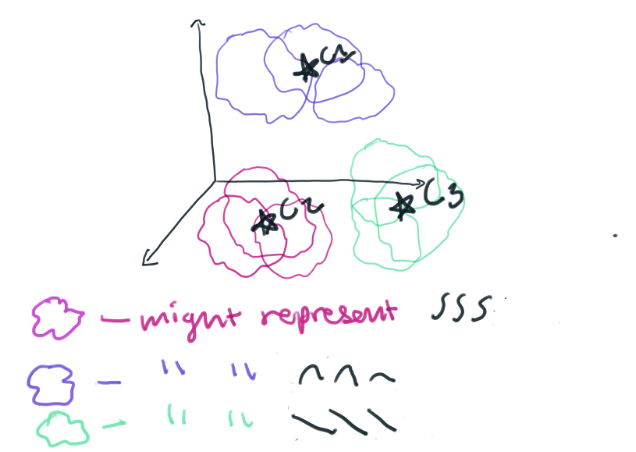
一个簇可能表示一个真正特定的多项式函数。簇也可以表示一个简单的多项式, 如 y=x^3。每个群集所代表的行类型由段大小决定。您的段大小越小, 您就越能将时间序列数据分解为组件片断-简单多项式。通过将我们的 segment_len 设置为 32, 我们将制作许多复杂的多项式。在某种程度上, 我们选择的簇数量将决定多项式的特定系数的重要意义。如果我们做了少量的簇, 系数就不会那么重要了。

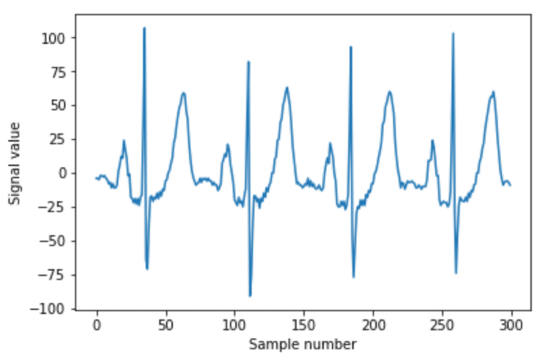
下面是用于窗口化数据的代码, 如下所示:

import numpy as np

segment_len = 32
slide_len = 2

segments = []
for start_pos in range(0, len(ekg_data), slide_len):
    end_pos = start_pos + segment_len
     segment = np.copy(ekg_data[start_pos:end_pos])
    # if we're at the end and we've got a truncated segment, drop it
    if len(segment) != segment_len:
        continue
    segments.append(segment)

我们的部分将如下所:

window_rads = np.linspace(0, np.pi, segment_len) window = np.sin(window_rads)**2 windowed_segments = [] for segment in segments: windowed_segment = np.copy(segment) * window windowed_segments.append(windowed_segment)

现在, 我们的所有部分将开始和结束的值为0。

2. 分组时间

from sklearn.cluster import KMeans

clusterer = KMeans(n_clusters=150)
clusterer.fit(windowed_segments)

我们的集群的质心可以从 clusterer.cluster_centers_ 。他们有 (150, 32) 的形状。这是因为每个中心实际上是32点的数组, 我们创建了150个集群。

3. 重建时间

首先, 我们做一个0s 的数组, 只要我们的异常数据集。(我们已经采取了我们的 ekg_data, 并创造了一个异常通过插入约 0s ekg_data_anomalous[210:215] = 0 )。我们将最终用预测的质心替换重建阵列中的0s。

#placeholder reconstruction array 
reconstruction = np.zeros(len(ekg_data_anomalous))

接下来, 我们需要将异常数据集分割为重叠段。我们将根据这些部分进行预测。

slide_len = segment_len/2
# slide_len = 16 as opposed to a slide_len = 2. Slide_len = 2 was used to create a lot of horizontal translations to provide K-Means with a lot of data. 

#segments were created from the ekg_data_anomalous dataset from the code above
for segment_n, segment in enumerate(segments):
    # normalize by multiplying our window function to each segment
    segment *= window
    # sklearn uses the euclidean square distance to predict the centroid
    nearest_centroid_idx = clusterer.predict(segment.reshape(1,-1))[0]
    centroids = clusterer.cluster_centers_
    nearest_centroid = np.copy(centroids[nearest_centroid_idx])

    # reconstructed our segments with an overlap equal to the slide_len so the centroids are       
    stitched together perfectly. 
    pos = segment_n * slide_len
    reconstruction[int(pos):int(pos+segment_len)] += nearest_centroid

最后, 确定我们是否有大于2% 的错误和情节。

error = reconstruction[0:n_plot_samples] - ekg_data_anomalous[0:n_plot_samples]
error_98th_percentile = np.percentile(error, 98)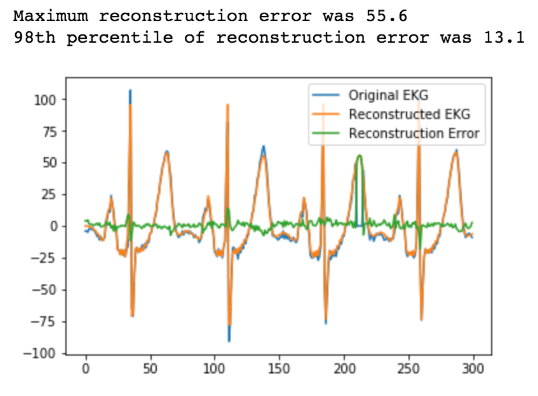

4. 警报

现在, 如果我们想提醒我们的异常, 我们所要做的就是设置一个阈值为13.1 的重建错误。每当它超过 13.1, 我们就发现了异常。

现在我们已经花了这么多时间学习和理解 k-手段及其在上下文异常检测中的应用, 让我们来讨论为什么使用它是个坏主意。为了帮助你完成这部分, 我将给你一个简短的大脑休息:

为什么不应该使用 K 手段进行上下文时间序列异常检测

我学到了很多关于使用 K 手段的缺点从这个帖子K 表示只收敛于局部极小值以找到质心

当 K 表示发现质心时, 它首先绘制150个随机的 “点” (在我们的例子中它实际上是一个32维的对象, 但是让我们把这个问题减少到一个2维的类比上)。它使用这个等式来计算所有150质心和其他所有 “点” 之间的距离。然后, 它需要查看所有这些距离, 并根据它们的距离将对象组合在一起。Sklearn 计算的距离与平方欧几里德差异(这是比仅使用欧几里德差异更快)。然后它根据这个等式更新质心的位置 (你可以认为它有点像从群集中的对象的平均距离)。

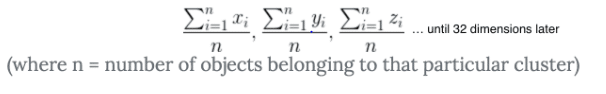
一旦无法更新, 它就决定了该点是质心。然而, K 的意思是不能真正 “看到森林通过树木。如果初始随机放置的质心在一个糟糕的位置, 那么 K 意味着不会分配一个正确的质心。相反, 它将收敛于本地最小值, 并提供较差的群集。由于聚类差, 预测不佳。要了解有关 K 方法如何找到质心的更多信息, 我建议您阅读此文章。看看这里, 了解更多关于 K 意味着如何收敛局部极小值的信息。

2. 每个 Timestep 都作为一个维度进行转换

如果我们的时间步骤是统一的, 那么这样做是很好的。但是, 试想一下, 如果我们使用 K 手段对传感器数据。假设您的传感器数据以不规则的间隔来进行。k-手段可以很容易地产生集群, 是你的基础时间序列行为的原型。

3. 用欧几里德距离作为相似性度量可以误导

仅仅因为对象接近质心并不意味着它应该属于该群集。如果您环顾四周, 您可能会注意到, 附近的其他对象都属于不同的类。相反, 您可以考虑使用 k-方法创建的群集中的对象应用 KNN。

我希望这和以前的博客帮助你在你的异常检测旅程。请让我知道, 如果你发现任何混淆或随时向我求助。你可以去 InfluxData社区网站或推我们 @InfluxDB。

Related Posts:

Tags: ,
Comments are closed.