Posted by on | Featured

在机器学习和深度学习领域，激活函数在神经网络做出复杂决策和预测的能力中发挥着关键作用。其中，softmax 激活函数脱颖而出，尤其是在结果相互排斥的分类任务中。本文深入探讨了 softmax 函数，深入探讨了其工作原理、应用以及在人工智能 (AI) 领域的重要性。

Softmax 激活函数

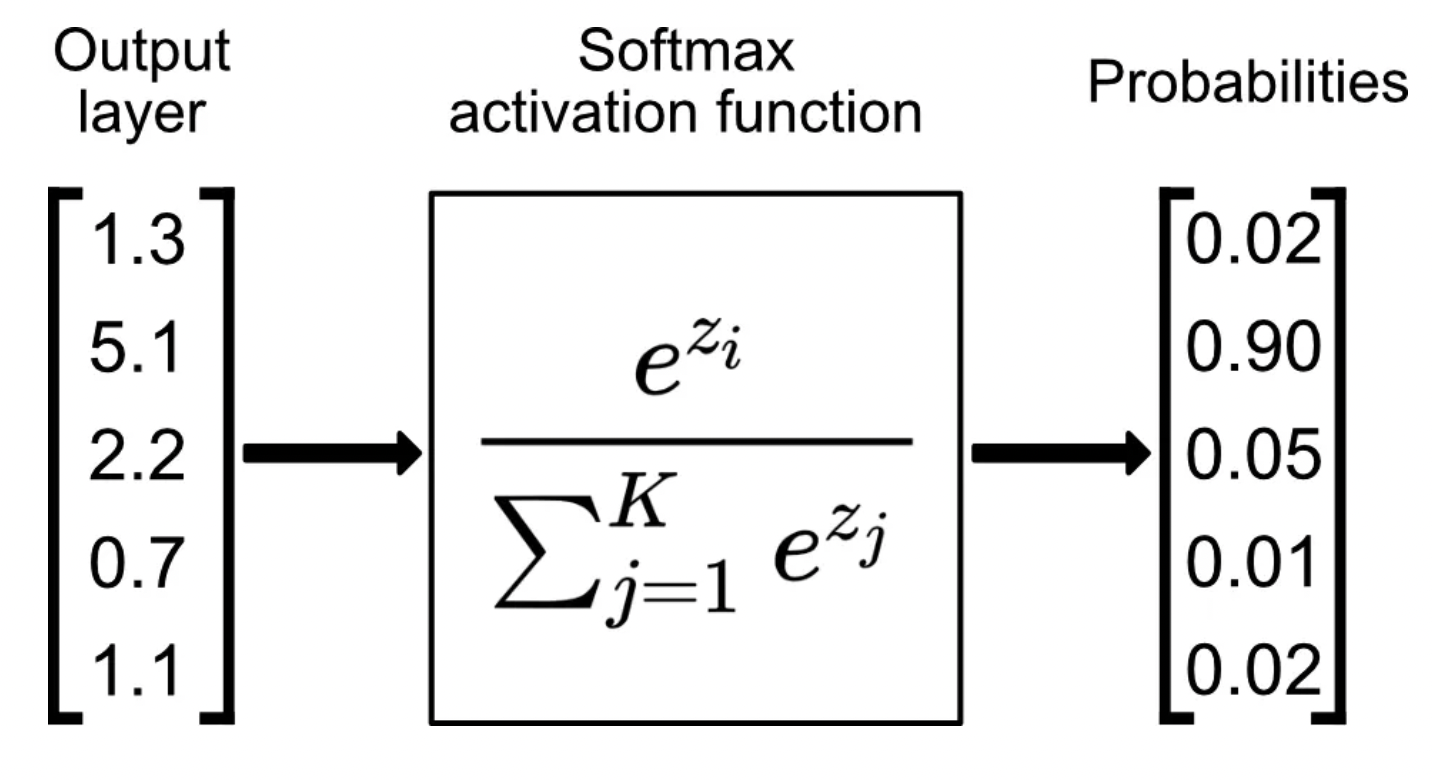图片来源：迈向数据科学图片来源：走向数据科学

softmax 函数通常用于分类任务的神经网络模型的最后一层，通过获取每个输出的指数并对这些值进行归一化，将原始输出分数（也称为 logits）转换为概率除以所有指数的总和。此过程确保输出值在 (0,1) 范围内且总和为 1，从而使它们可以解释为概率。

softmax函数的数学表达式如下：

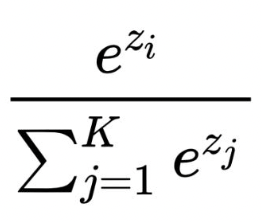
softmax function

这里，zi 表示第 i 类的 softmax 函数的输入，分母是输出层中所有原始类分数的指数之和。

想象一个神经网络，其任务是对手写数字 (0-9) 的图像进行分类。最后一层可能输出一个包含 10 个数字的向量，每个数字对应一个数字。然而，这些数字并不直接代表概率。 softmax 函数介入将此向量转换为每个数字（类别）的概率分布。

这是 Softmax 如何实现这一魔力的

  1. 输入：softmax 函数采用实数向量 z，表示神经网络最后一层的输出。
  2. 求幂：使用数学常数 e（大约 2.718）对 z 中的每个元素求幂。这确保所有值都变为正值。
  3. 标准化：然后将指数值除以所有指数值的总和。此归一化步骤保证输出值总和为 1，这是概率分布的关键属性。

Softmax 函数的属性

  • 输出范围：softmax 函数保证输出值位于 0 到 1 之间，满足概率的定义。
  • 概率总和：如前所述，softmax 函数所有输出的总和始终等于 1。
  • 可解释性：Softmax 将原始输出转换为概率，使网络的预测更易于理解和分析。

Softmax 激活的应用

Softmax 主要用于多类分类问题。从图像识别和自然语言处理（NLP）到推荐系统，它高效处理多个类别的能力使其不可或缺。例如，在预测水果类型的神经网络模型中，softmax 将帮助确定图像是苹果、橙子或香蕉的概率，确保这些概率的总和等于 1。

在 Python 中，我们可以按如下方式实现 Softmax：

Python

  

来自数学导入 exp

def softmax(输入向量):
    # 计算输入向量中每个元素的指数
    指数 = [exp(i) for i in input_vector]
    
    # 正确：将每个值的指数除以指数之和
    # 并四舍五入到小数点后 3 位
    指数之和 = sum(指数)
    概率 = [round(exp(i) / sum_of_exponents, 3) for i in exponents]
    
    返回概率

print(softmax([3.2, 1.3, 0.2, 0.8]))

输出如下：

output

与其他激活函数的比较

与 sigmoid 或 ReLU（整流线性单元）等用于隐藏层中进行二元分类或非线性变换的函数不同，softmax 特别适合多类场景中的输出层。虽然 sigmoid 将输出压缩在 0 和 1 之间，但它不能确保输出之和为 1——这使得 softmax 更适合概率。 ReLU 以解决梯度消失问题而闻名，但它不提供概率，这突显了 softmax 在分类上下文中的作用。

Softmax 实际应用：多类分类

Softmax 在多类分类问题中表现出色，其中输入可以属于多个离散类别之一。以下是一些现实世界的示例：

  • 图像识别：对物体、动物或场景的图像进行分类，其中每个图像可以属于特定类别（例如猫、狗、汽车）。
  • 垃圾邮件检测：将电子邮件分类为垃圾邮件或非垃圾邮件。
  • 情绪分析：将文本分为积极、消极或中性情绪等类别。

在这些场景中，softmax 函数提供网络预测的概率解释。例如，在图像识别中，softmax 输出可能表明图像有 70% 的概率是猫，30% 的概率是狗。

使用 Softmax 的优点

使用 softmax 激活函数有几个优点 – 以下是您可以从中受益的一些优点：

  • 概率分布：Softmax 为每个类别提供明确定义的概率分布，使我们能够评估网络对其预测的置信度。
  • 可解释性：与原始输出值相比，概率更容易理解和传达。这样可以更好地评估和调试神经网络。
  • 数值稳定性：softmax 函数具有良好的数值稳定性，使其能够高效地训练神经网络。

Softmax激活函数教程

让我们通过一个简单的教程来了解 softmax 激活函数是如何工作的。

让我们使用 SingleStore Notebook 功能来执行本教程。如果您还没有激活您的免费 SingleStore 试用版以开始使用笔记本。

注册后，转到“开发”选项并创建一个空白笔记本。

singlestore

新笔记本

为您的笔记本命名并开始添加以下说明。

本教程说明了如何根据一组 logits 计算 softmax 概率，展示其在将原始分数转换为总和为 1 的概率方面的应用。

第 1 步：安装 NumPy 和 Matplotlib 库

Python

  

!pip 安装 numpy
!pip 安装 matplotlib

第 2 步：导入库

Python

  

将 numpy 导入为 np
将 matplotlib.pyplot 导入为 plt

第 3 步：实现 Softmax 函数

使用 NumPy 实现 softmax 函数。此函数采用原始分数 (logits) 向量并返回概率向量。

Python

  

def softmax(logits):

    exp_logits = np.exp(logits - np.max(logits)) # 提高数值稳定性

    概率 = exp_logits / np.sum(exp_logits)

返回概率

第 4 步：创建一组 Logits

将一组 logits 定义为 NumPy 数组。这些 logits 可以是您想要转换为概率的任何模型输出的原始分数。

Python

  

logits = np.array([2.0, 1.0, 0.1])

第 5 步：应用 Softmax 函数

使用之前定义的 softmax 函数将 logits 转换为概率。

Python

  

概率 = softmax(logits)
print("概率：", 概率)

第 6 步：可视化结果

为了更好地理解 softmax 函数的效果，请使用 Matplotlib 可视化 logits 和生成的概率。

Python

  

# 绘图
标签 = ['1 类', '2 类', '3 类']
x = 范围(len(标签))

plt.figure(figsize=(10, 5))
plt. 子图(1, 2, 1)
plt.bar(x, logits, color='red')
plt.title('Logits')
plt.xticks(x, 标签)

plt. 子图(1, 2, 2)
plt.bar(x, 概率, color='绿色')
plt.title('Softmax 后的概率')
plt.xticks(x, 标签)

plt.show()

完整的教程代码可以在此存储库中找到。

softmax 函数是用于多类分类任务的神经网络的重要组成部分。它使网络能够做出概率预测，从而更细致地了解其输出。随着深度学习的不断发展，softmax 函数仍将是基石，在神经网络的原始计算和可解释概率的世界之间架起一座桥梁。

Tags: ,
Comments are closed.