了解主要组件分析 （PCA）

随着人工智能和机器学习领域的进步，了解这些技术背后的基础知识变得至关重要。本文将介绍主要分量分析，帮助您了解维度减少背后的概念，以及如何使用它来处理高维数据。

您可能还喜欢：
10 机器学习算法，你应该知道成为一个数据科学家

需要原理组件分析 （PCA）

通常，机器学习在为机器培训提供的数据集足够大且简洁时，会创造奇迹。通常，拥有大量数据可以让我们构建更好的预测模型，因为我们有更多的数据来训练计算机。但是，使用大型数据集有其自身的缺陷。最大的陷阱是维度的诅咒。

事实证明，在大型维度数据集中，要素中可能存在大量不一致，或者数据集中存在大量冗余要素，这只会增加计算时间，使数据处理和 EDA 更加复杂。

为了摆脱维度的诅咒，引入了一种称为维数减少的过程。尺寸减少技术只能用于筛选训练所需的有限数量的重要功能，这就是 PCA 的用处。

什么是主要组件分析？

主要组件分析 （PCA） 是一种维度缩减技术，使您能够识别数据集中的关联和模式，以便将其转换为尺寸显著较低的数据集，而不会丢失任何重要信息.

PCA 背后的主要思想是找出数据集中各种要素之间的模式和相关性。在发现不同变量之间的强相关性时，将最终决定减少数据的维度，以便仍然保留重要数据。

对于解决涉及使用高维数据集的复杂数据驱动问题，此过程非常重要。PCA 可通过一系列步骤实现。让我们讨论整个端到端流程。

PCA 的一步一步计算

使用 PCA 执行尺寸减少需要遵循以下步骤：

1. 数据标准化
2. 计算协方差矩阵
3. 计算功能向量和功能值
4. 计算主要组件
5. 减小数据集的尺寸

让我们详细讨论每个步骤：

第 1 步：数据标准化

如果您熟悉数据分析和处理，您就会知道错过标准化可能会导致有偏差的结果。标准化就是以所有变量及其值都在相似范围内的方式扩展数据。

举个例子，假设我们的数据集有 2 个变量，一个变量的值介于 10-100 之间，另一个变量的值介于 1000-5000 之间。在这种情况下，使用这些预测变量计算的输出将偏置，因为范围较大的变量将对结果产生更明显的影响。

因此，将数据标准化为可比较的范围非常重要

可以这样计算：

执行此步骤后，数据中的所有变量都跨标准和可比比例进行缩放。

第 2 步：计算协方差矩阵

如前所述，PCA 有助于识别数据集中功能之间的相关性和依赖关系。协方差矩阵表示数据集中不同变量之间的相关性。识别重相关变量至关重要，因为它们包含有偏差和冗余的信息，这会降低模型的整体性能。

在数学上，协方差矩阵是 p + p 矩阵，其中 p 表示数据集的维度。矩阵中的每个条目表示相应变量的协方差。

假设我们有一个包含变量 a 和 b 的 2 维数据集，协方差矩阵是 2×2 矩阵，如下所示：

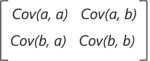以下是协方差矩阵中的关键要点：

• 协方差值表示两个变量相对于彼此的相互依赖程度
• 如果协方差值为负，则表示各自的变量彼此间接成正比
• 正协方差表示各自的变量彼此成正比

简单的数学，不是吗？现在，让我们继续，看看 PCA 中的下一步。

第 3 步：计算 Eigen 向量和 Eigen 值

Eigenvectors 和 igenvalue 是必须从协方差矩阵计算以确定数据集的主要分量的数学构造。

但首先，让我们进一理解主要组件

什么是主要组件？

简而言之，主要组件是从初始变量集中获得的新变量集。主要分量的计算方式使新获得的变量非常重要且彼此独立。主要组件压缩并拥有分散在初始变量中的大部分有用信息。

如果数据集为 5 个维度，则计算 5 个主体组件，这样，第一个主体组件存储最大可能的信息，第二个主体组件存储剩余的最大信息，等等，您就会得到这个想法。

现在，Eigenvectors 会从属于整个过程的什么？

假设你们对Eigenvectors和igenvalue都有基本的了解，我们知道这两个代数公式总是作为一对计算，也就是说，对于每个前向量都有一个基因值。数据中的维度确定需要计算的 iigenvector 的数量。

考虑一个二维数据集，计算两个功能向量（及其各自的功能值）。igenvector 背后的思想是使用协方差矩阵来了解数据中方差最多的位置。由于数据中的更多方差表示有关数据的详细信息，因此使用 iigenvector 来标识和计算主要组件。

另一方面，Eigenvalue只是表示各位向量的标量。因此，功能向量和功能值将计算数据集的主要组件。

第 4 步：计算主要组件

一旦我们计算了 Eigenvectors 和 igenvalue，我们要做的就是按照降序排列它们，其中具有最高值的 iigenvector 最为重要，从而形成第一个主体分量。因此，可以删除意义较小的主要组件，以减少数据的维度。

计算主要组件的最后一步是形成一个矩阵，称为特征矩阵，其中包含包含有关数据的最大信息的所有重要数据变量。

第 5 步：减小数据集的维度

执行 PCA 的最后一步是重新排列原始数据与表示数据集的最大和最重要的信息的最终主体组件。为了用新形成的主要分量替换原始数据轴，只需将原始数据集的转置乘以获得的特征矢量的转置是时候弄脏你的手，并使用真实的数据集执行所有这些步骤了。

使用 Python 的主要组件分析

在本节中，我们将使用 Python 执行 PCA。

问题陈述：执行分步执行主体组件分析，以减少数据集的维度。

数据集 描述：包含大约 9000 部电影（功能）的 700 多个用户分级的电影分级数据集。

逻辑：通过查找数据中最重要的功能来执行 PCA。PCA 将按照上面定义的步骤执行。

让我们开始吧！

第 1 步：导入所需包

import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from matplotlib import*
import matplotlib.pyplot as plt
from matplotlib.cm import register_cmap
from scipy import stats
from sklearn.decomposition import PCA as sklearnPCA
import seaborn

步骤 2：导入数据集

#Load movie names and movie ratings
movies = pd.read_csv('C:UsersNeelTempDesktopPCA DATAmovies.csv')
ratings = pd.read_csv('C:UsersNeelTempDesktopPCA DATAratings.csv')
ratings.drop(['timestamp'], axis=1, inplace=True)

第 3 步：格式化数据

def replace_name(x):
return movies[movies['movieId']==x].title.values[0]
ratings.movieId = ratings.movieId.map(replace_name)
M = ratings.pivot_table(index=['userId'], columns=['movieId'], values='rating')
m = M.shape
df1 = M.replace(np.nan, 0, regex=True)

第 2 步：标准化

在下面的代码行中，我们使用 sklearn 包提供的 StandardScalar（） 函数，以便在可比较的范围内扩展数据集。如前所述，需要标准化以防止最终结果中的偏见。

X_std = StandardScaler().fit_transform(df1)

第 3 步：计算协方差矩阵

如前所述，协方差矩阵表示数据集中不同要素之间的相关性。识别重相关变量至关重要，因为它们包含有偏差和冗余的信息，这会降低模型的整体性能。

以下代码段计算数据的协方差矩阵：

mean_vec = np.mean(X_std, axis=0)
cov_mat = (X_std - mean_vec).T.dot((X_std - mean_vec)) / (X_std.shape[0]-1)
print('Covariance matrix n%s' %cov_mat)

Covariance matrix
[[ 1.0013947 -0.00276421 -0.00195661 ... -0.00858289 -0.00321221
-0.01055463]
[-0.00276421 1.0013947 -0.00197311 ... 0.14004611 -0.0032393
-0.01064364]
[-0.00195661 -0.00197311 1.0013947 ... -0.00612653 -0.0022929
-0.00753398]
...
[-0.00858289 0.14004611 -0.00612653 ... 1.0013947 0.02888777
0.14005644]
[-0.00321221 -0.0032393 -0.0022929 ... 0.02888777 1.0013947
0.01676203]
[-0.01055463 -0.01064364 -0.00753398 ... 0.14005644 0.01676203
1.0013947 ]]

第 4 步：计算 Eigen 矢量和 Eigen 值

在此步骤中，计算功能向量和功能值，这基本上计算了数据集的主要分量。

#Calculating eigenvectors and eigenvalues on covariance matrix
cov_mat = np.cov(X_std.T)
eig_vals, eig_vecs = np.linalg.eig(cov_mat)
print('Eigenvectors n%s' %eig_vecs)
print('nEigenvalues n%s' %eig_vals)

Eigenvectors
[[-1.34830861e-04+0.j 5.76715196e-04+0.j 4.83014783e-05+0.j ...
5.02355418e-14+0.j 6.48472777e-12+0.j 6.90776605e-13+0.j]
[ 5.61303451e-04+0.j -1.11493526e-02+0.j 8.85798170e-03+0.j ...
-2.38204858e-11+0.j -6.11345049e-11+0

39454110e-12[0.j]
• 4.58686517e-04_0.j -2.39083484e-03_0.j 6.58309436e-04_0.j …
-7.00290160e-12_0.j -5.53245120e-12_0.j 3.35918400e-13_0.j_
…
• 5.22202072e-03_0.j -5.49944367e-03_0.j 5.16164779e-03_0.j …
2.53271844e-10=0.j 9.69246536e-10=0.j 5.86126443e-11=0.j*
• 8.97514078e-04_0.j -1.14918748e-02_0.j 9.41277803e-03_0.j …
-3.90405498e-10_0.j -7.88691586e-10=0.j -2.80604702e-11=0.j*
• 4.36362199e-03_0.j -7.90241494e-03_0.j -7.48537922e-03_0.j …
-6.38353830e-10_0.j -6.47370973e-10=0.j 1.4147483e-13_0.j_*

特征
* 1.54166656e_03_0.j 4.23920460e_02_0.j 3.19074475e_02_0.j …
8.84301723e-64_0.j 1.48644623e-64_0.j-3.46531190e-65_0.j_

步骤 7：计算要素矢量

在此步骤中，我们按降序重新排列功能值。这表示主要组件的显著性，按降序排列：

# Visually confirm that the list is correctly sorted by decreasing eigenvalues
eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))]
print('Eigenvalues in descending order:')
for i in eig_pairs:
print(i[0])

Eigenvalues in descending order:
1541.6665576008295
423.92045998539083
319.07447507743535
279.33035758081536
251.63844082955103
218.62439973216058
154.61586911307694
138.60396745179094
137.6669785626203
119.37014654115806
115.2795566625854
105.40594030056845
97.84201186745533
96.72012660587329
93.39647211318346
87.7491937345281
87.54664687999116
85.93371257360843
72.85051428001277
70.37154679336622
64.45310203297905
63.78603164551922
62.11260590665646
60.080661628776205
57.67255079811343
56.490104252992744
55.48183563193681
53.78161965096411

....

第 5 步：使用 PCA（） 函数降低数据集的维码

以下代码段使用 sklearn 包提供的预定义 PCA（） 函数来转换数据。n_components参数表示要将数据适合的主要组件数：

pca = PCA(n_components=2)
pca.fit_transform(df1)
print(pca.explained_variance_ratio_)

[0.13379809 0.03977444]

输出显示 PC1 和 PC2 约占数据集方差的 14%。

步骤 6：投影方差 w.r.t 原则组件

为了深入了解数据相对于不同数量的主要组件的方差，让我们绘制一个 scree 绘图。在统计信息中，scree 图表示与每个主要分量关联的方差：

pca = PCA().fit(X_std)
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance')
plt.show()

有了这个，我们来到这个博客的结尾。如果您对本主题有任何疑问，请发表评论。

进一步阅读

初学者数据分析原理

尺寸减少技术：从哪里开始