用绳子打结,把两端连在一起。在绳索的每个点上,计算曲率(即绳索弯曲多少,并将其集成在绳索的长度上)。法里-米尔诺定理说结果必须大于4°。这篇文章将通过计算数字积分结的曲率来说明这个定理。
您可能还喜欢:名声、困难和有用性。
如果p和q是相对的质数整数,则以下方程将一个结参数化。
x(t) = cos (pt) ( cos (qt) = 2)
y(t) = 辛 (pt) ( cos (qt) = 2)
z(t) = -sin (qt)
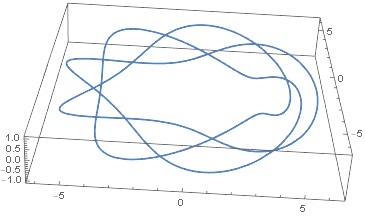
事实上,这是一个圆环结,因为曲线停留在圆环(圆环)的表面。例如,通过设置p = 2 和q = 3,我们可以获得一个颤合结。
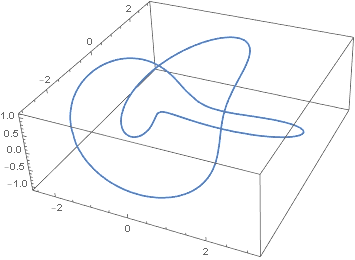
我们将使用Mathematica计算此结和其他示例的总曲率。首先参数化:
x[t_, p_, q_] := Cos[p t] (Cos[q t] + 2)
y[t_, p_, q_] := Sin[p t] (Cos[q t] + 2)
z[t_, p_, q_] := -Sin[q t]我们可以绘制的圆环,如下所示:
k[t_, p_, q_] := {
x[t, p, q],
y[t, p, q],
z[t, p, q]
}
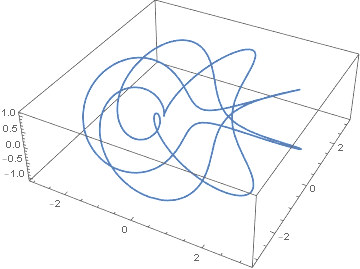
ParametricPlot3D[k[t, p, q], {t, 0, 2 Pi}]这里有一个更复杂的结与p = 3和q = 7。
在将曲率与弧长度集成之前,我们需要一个圆弧长度元素的表达式作为参数t的函数。
ds[t_, p_, q_] := Sqrt[
D[x[t, p, q], t]^2 +
D[y[t, p, q], t]^2 +
D[z[t, p, q], t]^2
]现在,我们可以计算总曲率。
total[p_, q_] := NIntegrate[
ArcCurvature[k[t, p, q], t] ds[t, p, q],
{t, 0, 2 Pi}
]我们可以用它来发现,总曲率的(2,3)圆环结,trefoil,是17.8224,而4+是12.5664。因此,法里-米尔诺定理持有。
让我们再举一个例子,这次是1,4个结。
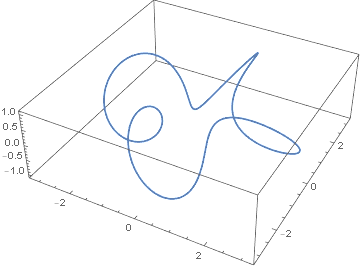
你可以看到,这实际上不是结。这与我们上面所说的并不矛盾,因为 1 和 4 不是相对黄金。
当我们计算其总曲率时,我们得到24.2737,超过4°。Fary-Milnor 定理没有说总曲率超过 4° 是循环打结的充分条件;它说这是必要的
如果用较大的数字更改参数化中的 2,则从图形中更容易看到曲线位于圆环上。例如,如果我们再次绘制 (3,7) 结,将 2 替换为 5,我们可以在结内看到一个圆环。
ParametricPlot3D[
{Cos[3 t] (5 + Cos[7 t]),
Sin[3 t] (5 + Cos[7 t]),
Sin[7 t]}, {t, 0, 2 Pi}]