英金只是在空中翻动一枚硬币。我们的生活能被这样简单的行动所定义吗?据统计, 答案是 “是”。在我上学的时候, 我一直在想, “为什么要抛硬币来学习统计?与现实生活有什么关系? “基本上没有人说这是一个简单的现实生活模拟。怎么会这样?想想你的生活当你申请一份工作时, 只有两个结果: 你会得到这份工作, 否则你不会。另一个例子, 从垃圾桶里拉一个球。一家公司有许多员工。在特定的时刻, 一名员工可以离开公司, 新员工可以开始新的工作。这可以是一个模拟更换一个球在垃圾桶。到目前为止, 概率是所有简单事件的焦点。回到学生的问题在这篇文章中, 没有人翻转硬币或拉出一个球从垃圾桶。这些只是对我们基本生活的基本模拟。
现在, 主要问题是: 是否有可能定义所有此类事件?答案很简单, “没有”。因为没有办法知道你关注的所有事件。你无法接触到所有寻找工作的人, 估计他们是否会被接受这份工作。你必须对你能真正接触到的人感到满意。这就是所谓的 “样本”。如果我们能定义, 那么所有的质量是多少?它也被称为 “人口”。我们的结论是, 在统计学世界, 现实是 “样本”, 梦想是 “人口”。
这可以在下图中说明。
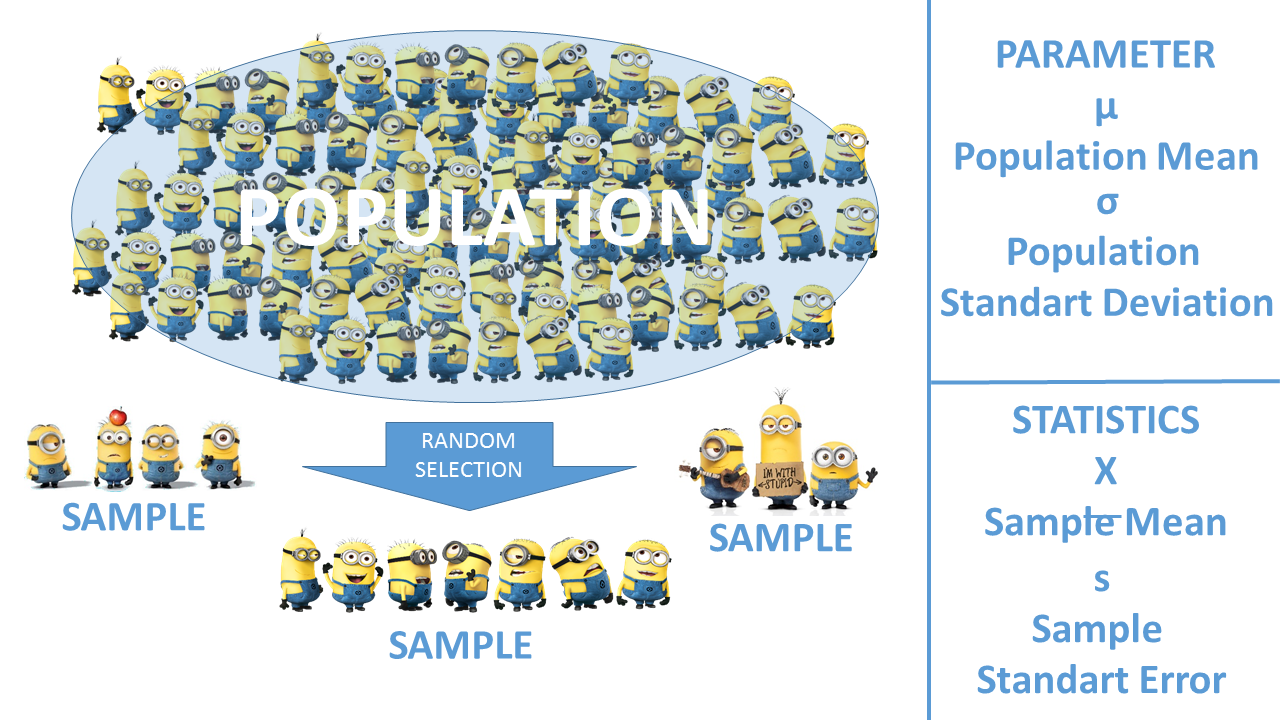
通过使用统计方法, 我们通过 “样本” 深入了解 “人口”, 因为我们知道 “样本” 的平均值, 并且我们可以计算 “样本” 集中预期事件的比例。统计旅程的第一步从这里开始。
然后, 让我们继续使用 “示例” 集。到目前为止, 我已经试图说, 我们可以用样本统计来预测人口参数。那是什么意思?如果我们有一些来自一个群体的样本数据, 我们可以通过使用该样本数据集预测其他一些样本值。这称为 “简单线性回归”。
这里可以找到一个更正式的定义: “简单线性回归是一种统计方法, 它允许我们总结和研究两个连续 (定量) 变量之间的关系。
简单的线性回归
正如我上面所说, 简单的线性回归给出了响应和预测值之间的统计关系。它不是像摄氏度和华氏转换这样的确定性关系。一个确定性关系只是通过下面的方程给出的, 它在两个因变量和自变量之间没有转换误差:
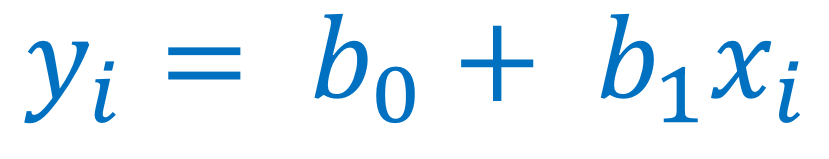
对于统计关系, 可以给出一个例子, 即 “avg. 温度” 和 “avg. 雨天” 之间的关系, 这将在本文中使用。小数据集如下表所示。有12个样本分别以类似的方式表示每个月的平均气温和平均雨天。
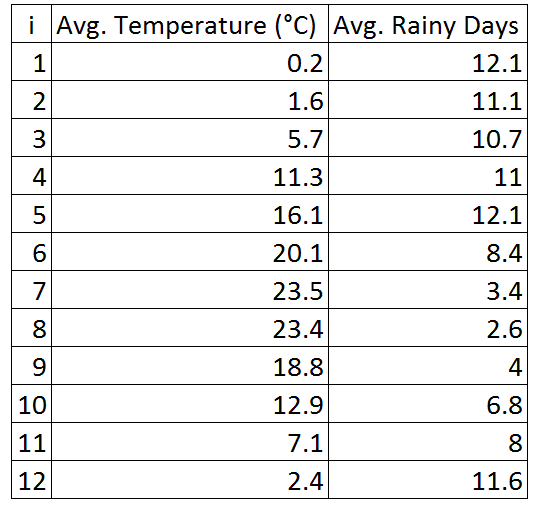
根据这些数据, 我们可以尝试预测平均温度 (x) 的其他可能值的平均雨天 (y)如果两个变量之间存在统计关系, 则必须存在 “预测误差”。简单线性回归中的预测误差是预测值和实际值之间的差异, 如下所示:

我们必须最小化预测的错误值, 以获得变量之间的 “最佳拟合线”。下面是简单线性回归的主要问题: “响应变量和预测变量之间的最佳拟合线是什么?”为什么我们需要最大限度地减少错误?答案可以从下面定义简单线性回归线的方程中看出。

为了使用给定的公式找到最佳拟合线, 我们必须计算 b0 和 b0 的值, 使平方预测误差之和成为最小的预测误差之和。为了简单起见, 我将不在这里进行公式计算。然而, 可以看出, 主要的想法是, 由于我们并不是所有关于人口的知识, 估计新值的准确性取决于从样本数据中获得最小的误差。当然, 您不必手动进行所有计算。有很多统计程序, 包括 excel, 您可以使用这些程序来计算错误。但重要的是要知道计算值是什么, 如何使用它们来控制模型, 以及应该如何解释它们。
Stastical jargon
| Sst | 平方合计 |
| Sse | 正方形的错误总和 |
| rs3 | 正方形的回归和 |
| r 平方 | 测定系数 |
| s | 估计的标准错误 |
r-平方: 因变量中的变化的百分比, 用最小二乘法线解释, 称为 r 平方值。对于一个独立变量, 高 r 平方值表示更适合。为了提高估计精度, 应考虑标准误差 (s)。
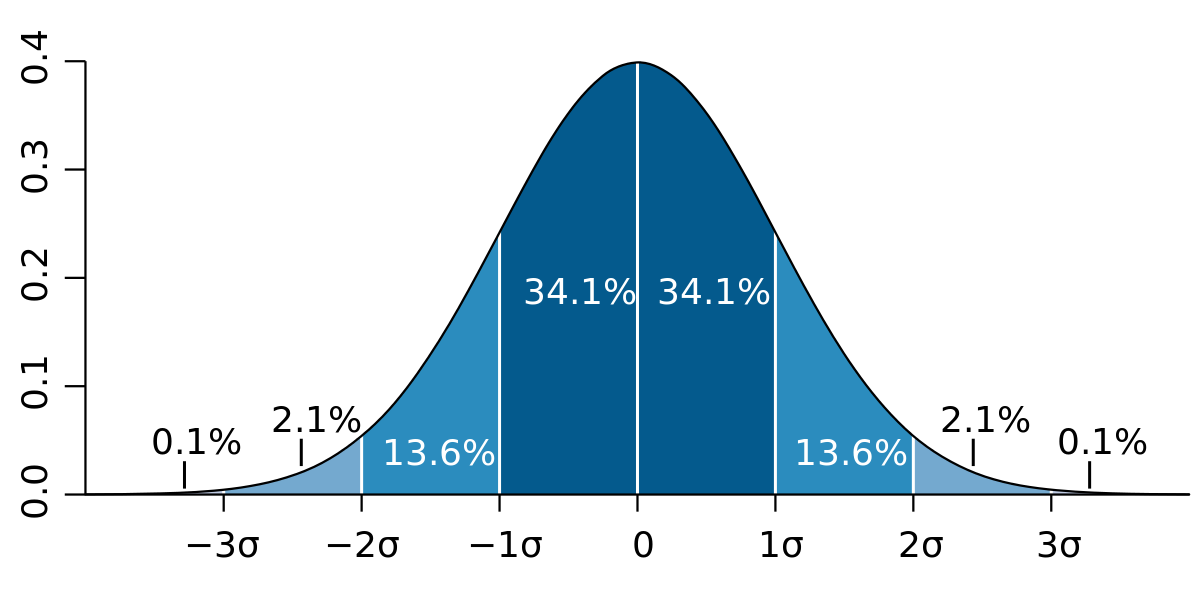
回归 (估计) 的标准误差 (s): 它测量最小二乘线周围点的传播。为了获得正态分布, 68% 的样本值应该根据最小二乘法的回归而成一个标准误差的边缘, 大约95% 的值应该在回归值的两个标准误差的边距内。这可以用下面的图表来说明 (从维基百科标准偏差页);
excel 的一个简单示例
现在让我们来看看一个简单的练习, 一个非常简单的数据集。我们将使用上面给出的数据集, 其中包括平均温度和雨天数。
步骤 1: 将数据放入 excel 工作表中。第一列应该是 x 轴值的 “平均温度 (°c)”, 第二列应该是 “平均. 雨天”。然后使用光标选择这两个选项, 如下图所示。从 “插入” 菜单中, 从图形类型中选择 “散点图” 图形。你会得到可以在图中看到的图形。
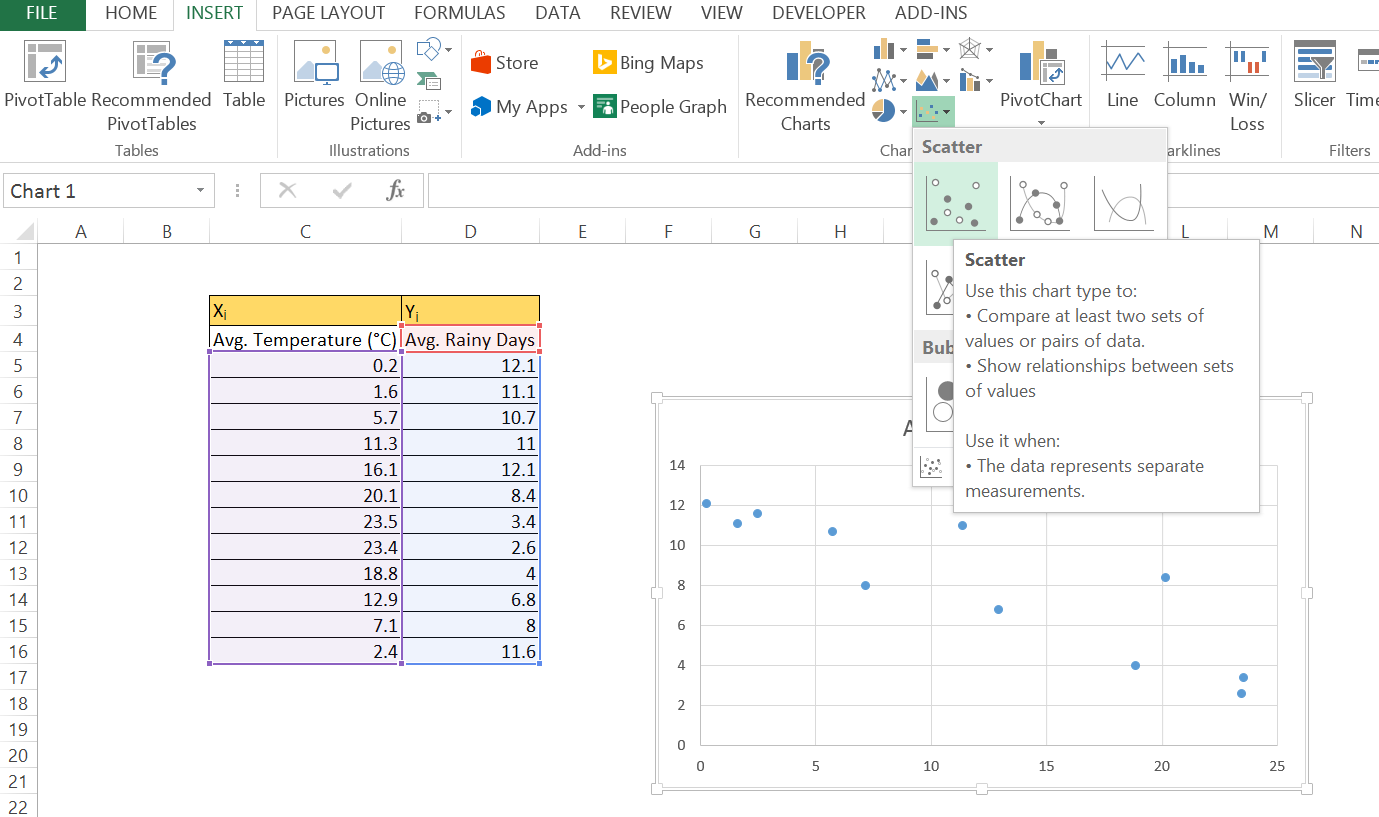
步骤 2: 要添加趋势线, 只需在图形上选择一个数据点cheeli.com.cn/wp-content/uploads/2018/11/10665997-add-trendline.png “width=”547″/>
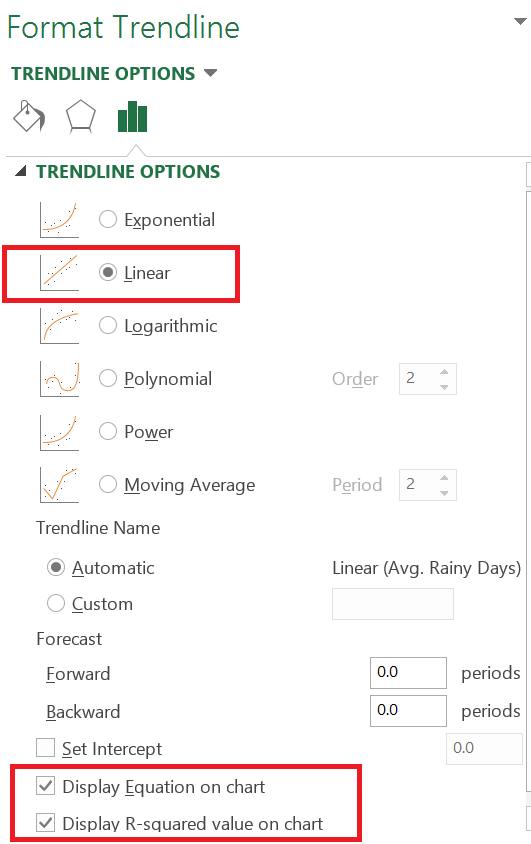
步骤 3: 趋势线的格式选项如下图所示。从选项中选择 “线性” 选项、”在图表上显示公式” 和 “在图表上显示 r 平方值”。
步骤 4: 您将得到以下图表:
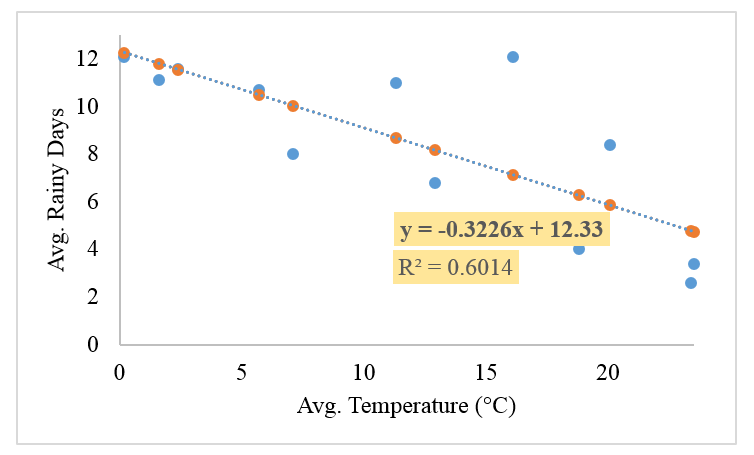
第5步: 该公式为此样本集提供了 “简单线性回归” 最适合的线。通过使用此公式, 您可以获得示例数据集的错误 (残差):
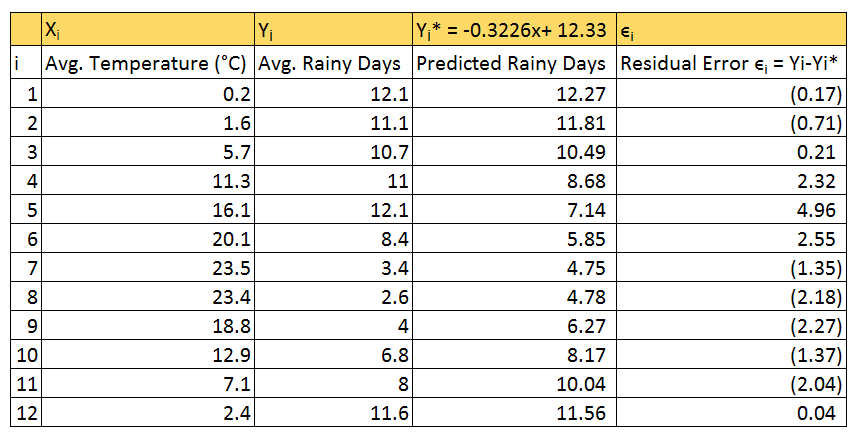
步骤 6: 要计算回归的标准误差, 请使用 excel 中的stexy(已知的 y, 已知的 x) 函数。对于 “已知的 y” 参数, 选择 “平均雨天” 列, 对于 “已知 x” 参数, 选择 “平均温度 (°c)”。当您运行公式时, 您将获得 ser 的值 (回归的标准错误): 2.341960944。
此值显示83% 的点位于最小二乘线的一个 ser 内。对于 r 平方值 “0.6014”, 线性关系解释了 “平均雨天” 中60% 的变化。
这只是旅程的开始…..。
