翻译整理 | One 本期编辑 | 一只小绿怪兽
译者简介:西南财经大学应用数学本科,英国曼彻斯特大学金融数学硕士,金融分析师,专注于利用数据建立金融模型,发掘潜在投资价值。
作者:Mirko Stojiljkovic
线性回归是统计学和机器学习的基础之一。无论是做统计,机器学习还是科学计算,都可能用上线性回归。因此,建议先掌握线性回归,然后再学习更复杂的方法。
通过阅读本文,你将了解到:
· 什么是线性回归
· 线性回归的用途
· 线性回归的原理
· 在Python中实现线性回归
01
什么是回归
回归主要用于研究变量之间的关系。例如,可以通过观察一些公司的职员,并试着了解他们的特征如何影响他们的薪水,比如经验,教育水平,职位,工作地点等等。
这就个回归问题,与每个职员相关的数据都是代表一次观察。其中职员的经验,教育水平,职位,工作地点都是独立的特征,这些特征决定了职员的薪水水平。
类似的,也可以试着建立房屋价格与地域,卧室数量,到市中心距离的数学依赖关系。
在回归分析中,经常会发现一些有趣的现象和一些观察,每次观察都会有两个或者更多的特征。假设其中一个特征依赖其他几个特征,可以试着去建立回归发现特征之间的关系。
换种说法,就是需要找到一个能够很好地将某些特征映射到其他特征的函数。依赖特征称为因变量,独立特征称为自变量。
回归模型中通常有一个连续且无界的因变量。但是,自变量可以是连续的,离散的,甚至是像性别,国籍,品牌等分类数据。
通常用y表示因变量,x表示自变量。如果有两个或者多个自变量,可以用向量x=(x1, …, xr)表示。
02
回归的用途
通常,回归被用来回答某些现象是否会对其他现象产生影响,或者说,几个变量之间是否存在关联。例如,可以用回归的方法确定工作经验或者性别是否在某种程度上影响到工资水平。
用新的自变量数据集去预测因变量时,回归也是非常有用的。举个例子,已知室外气温,一天的某个时间,以及家里居住的人数,可以试着预测下一个小时的家庭用电量。
回归可用于许多领域:经济,IT,社会科学等等。随着大量数据的可获取性提升以及人们对于数据的实用价值认知的提高,回归变得越来越重要了。
03
线性回归的原理
线性回归是被广泛使用的回归方法中比较重要的一种。它是最基础也是最简单的回归方法。它的主要优点是易懂。
原理
在对一组自变量x=(x1,…,xr)和因变量y进行回归时,我们假设y与x的关系:y=β0+β1x1+···+βrxr+ε。这个方程叫做回归方程。β0,β1,… ,βr是回归系数, ε是随机误差。
线性回归计算回归系数的估计值,或者说计算以b1,b2,…,br表示并用于预测的权重。其中回归函数被定义为f(x)=b0+b1x1+b2x2+···+brxr。回归函数可以很好地捕获自变量与因变量的依赖关系。
对于每一次观测i=1,…,n,回归函数f(xi)应该要足够接近实际观测的因变量yi值,其中yi与f(xi)的差值称为残差。回归是为了找到最优权重并用于预测,而残差最小的时候说明回归函数f(xi)与实际观测的yi是最接近的,此时对应的权重便是最优权重b=(b1,b2,…,br)。
通常使用最小化残差平方和的方法来计算最优权重,即最小化SSR=∑i(yi-f(xi))2。这种方法叫做最小二乘法OLS。
评价回归模型
实际观测值yi的变化一部分由于自变量xi的变化导致的。但是实际观测值yi仍然会有无法用回归函数f(xi)解释的部分。
而决定系数R2,用来说明实际观测值yi中有多大程度可以由回归函数f(x)解释。R2越大,两者拟合程度越高,意味着观测值yi-xi数据组可以很好的契合回归函数f(x)。
R2=1时,即SSR=0,称作完全拟合,这意味着所有yi-xi可以完全匹配回归函数f(x)。
单变量线性回归
单变量线性回归是线性回归中最简单的一种情形,即回归模型中只有一个自变量x=x1。
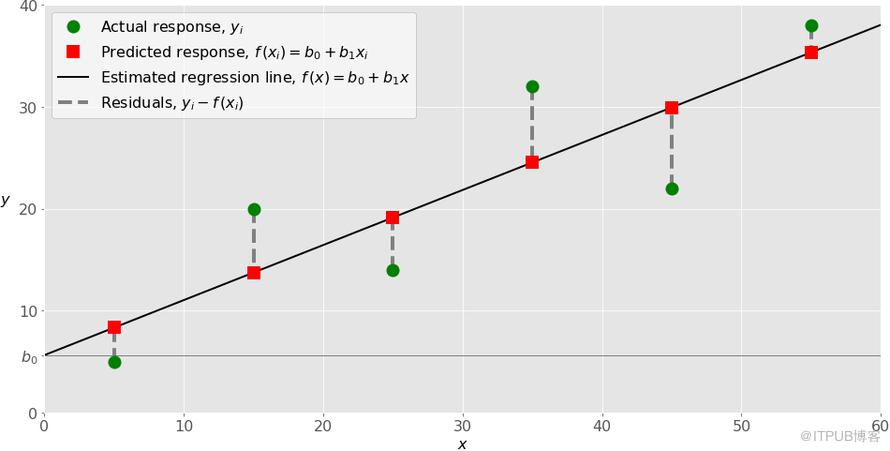
这些数据集一般来自实际业务中的数据采集。上图中,最左边绿点x=5,y=5就是观测值。
回归函数以图中黑线表示,其表达式为f(x)=b0+b1x。我们需要用最小化残差平方和SSR的方法来计算回归函数中的权重b0与b1。其中b0为截距,即回归函数f(x)与y轴的交点。b1为回归函数的斜率,也可以理解为黑线的倾斜程度。
图中红色方块表示的是xi-f(xi)的数据集,该数据集都落在直线上。例如x=5,f(5)=8.33。
有了以上两组数据后,便可以计算残差,即yi-f(xi)=yi-b0-b1xi,i=1,…,n。在图中残差可表示为绿点到红方块的距离,用虚线表示。在执行线性回归时,事实上是在试着使图中绿点到红方块的虚线总长度最小,即残差最小。
多变量线性回归
假如仅有两个自变量,回归函数可以写成f(x1,x2)=b0+b1x1+b2x2。这个函数在三维空间中是一个平面。
这种回归的目标也是确定权重b0,b1,b2,即使得这个平面f(x1,x2)与实际观测的数值间的距离最小,即最小化SSR。
两个自变量以上的多变量回归也与上述的方法类似。例如f(x1,…,xr)=b0+b1x1+···+brxr,这个方程中有r+1个权重bi需要估计。
多项式回归
可以将多项式回归视为线性回归的一般情形。自变量与因变量的多项式依赖关系可以通过回归得到多项式回归函数。
换句话说,回归函数f中,除了包含线性部分如b1x1,还可以加入非线性部分如b2x12,b3x13,甚至b4x1x2,b5x12x2等等。
单变量多项式回归是其中最简单的一种形式,例如2阶单变量多项式回归函数:f(x)=b0+b1x+b2x2。。
现在只需要通过最小二乘法计算b0,b1,b2即可。与上一节的线性回归函数f(x1,x2)=b0+b1x1+b2x2相比较,两种回归非常相似,并且都需要估计系数b0,b1,b2。因此,只需要将高阶项如x2视为因变量,多项式回归与普通的线性回归是一样的。
在2阶多变量的情形中,回归函数可以像这样:f(x1,x2)=b0+b1x1+b2x2+b3x12+b4x1x2+b5x22,回归的方法和前面叙述的一样。对五个自变量应用线性回归:x1,x2,x12,x1x2,x22。回归的结果得到6个在SSR最小化时的权重:b0,b1,b2,b3,b4,b5。
欠拟合和过拟合
在执行多项式回归中,一个需要引起高度重视的问题是:关于多项式回归函数最优阶数的选择。
阶数的选择并没有明确的规则。它需要视情况而定。但是,在选择阶数的时候,需要关注两个问题:欠拟合与过拟合。
当模型无法准确的捕获数据之间的依赖关系时导致欠拟合,这通常是由于模型过于简单导致的。欠拟合的模型在用现有数据进行回归时会有较低的决定系数R2,同时它的预测能力也不足。
当数据和随机波动性都拟合到模型中时会导致过拟合。换种说法,就是模型和现有数据契合程度过高了。高度复杂的模型一般都有很多自变量,这通常容易导致模型过拟合。将现有数据拟合这种模型的时候一般会有很高的决定系数R2。但是在使用新数据时,模型可能会表现出很弱的预测能力和低决定系数R2。
下图分别展示了欠拟合,好的拟合,和过拟合的模型:
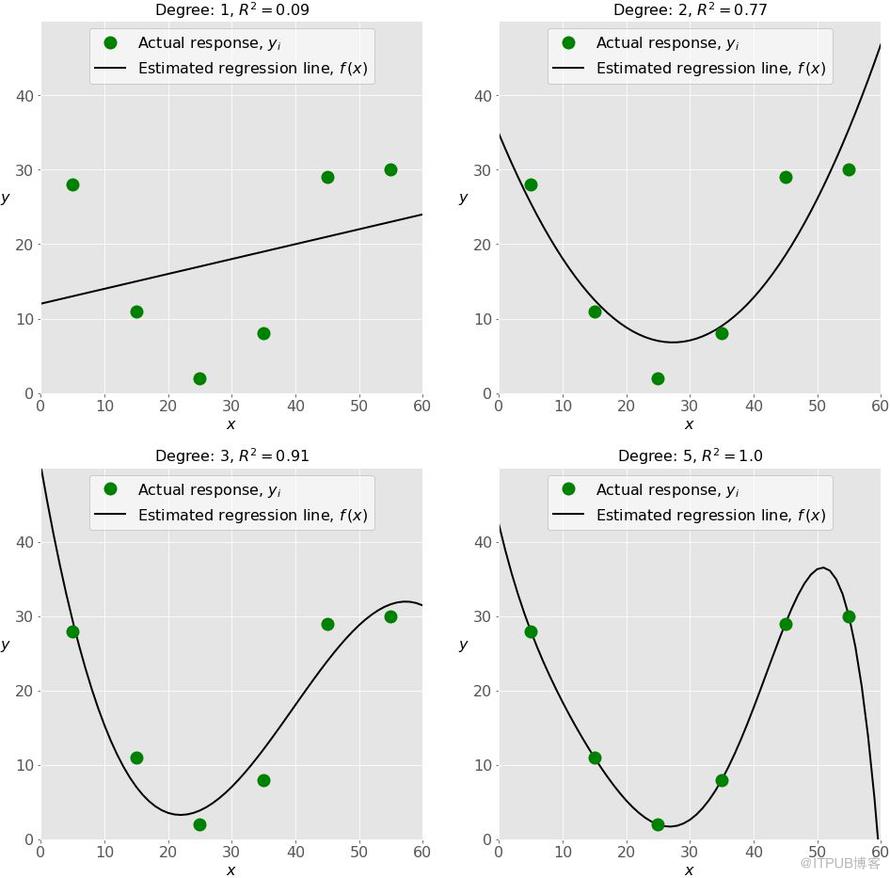
左上图是个低决定系数R2的线性回归。这条直线没有考虑当x变化时观测值yi的剧烈变动。这也许是一个欠拟合的例子。
右上图是个2阶多项式回归。在这个回归模型中,2阶也许是拟合该组数据的最优阶数。这个回归模型的R2还不错,并且可以很好地勾勒出了数据的趋势。
左下图是个3阶的多项式回归。回归模型的R2比右上图的要高。对于现有的数据,这个模型比右上图的模型要好。但是,它可能有一些过拟合的迹象,尤其是在x接近60的时候,现有的观测数据并没有显示出回归模型中给出的下降趋势。
最后,在右下图中,这是一个完全拟合,6个观测值都落在回归模型的曲线上。这可能是我们想要的回归模型,但是在多数情况下,这是一种过拟合的模型。它可能会有糟糕的预测能力。在这例中,可以看到曲线在x大于50时候毫无征兆的急速下降,并且在x=60附近归零。这种曲线可能是过度学习或者过度拟合现有数据导致的。
04
在Python中实现线性回归
关于线性回归Python库
numpy是一款基础Python包,它可以在单维和多维数组上进行高效的操作。它还提供很多数值计算方法,同时也是开源库。
如果不熟悉numpy,可以阅读官方的numpy使用指南,此外还有numpy相关的文章会在附录中提供。网络上还有大量的numpy资料可供搜索。
scikit-learn是一个被大量用户用于机器学习的Python库,该库是基于numpy和其他库建立的。它可以执行数据预处理,降维,回归,分类和聚类等功能。和numpy一样,scikit-learn也是开源的。
可以在scikit-learn官网上查看Generalized Linear Models页面了解更多关于线性模型的内容以进一步了解该库的原理。
statsmodels库可以实现一些在做线性回归时scikit-learn中没有的功能。它也是一个不错的Python库,主要用于统计模型的估计,模型的测试等等。同时它也是开源的。
基于sklearn的单变量线性回归
这里从最简单的单变量线性回归开始,手把手教你在Python中做线性回归模型,整个过程大致分五个基本步骤:
① 导入相关库和类
② 读取相关数据,对数据进行适当处理
③ 创建回归模型并对现有数据样本进行拟合
④ 查看模型的拟合结果,判断模型是否合理
⑤ 用模型进行预测
这几个步骤在大多数回归方法中基本是通用的。
Step 1:导入相关库和类
首先导入pandas,tushare库和sklearn.linear_model中的LinearRegression类:
import pandas as pd
import numpy as np
import tushare as ts
from sklearn.linear_model import LinearRegression当然,也可以用numpy库。pandas和numpy的数据类型可以与sklearn无缝对接,并且高效,可读性强。而类sklearn.linear_model.LinearRegression提供了执行线性回归的相关功能。
Step 2:读取数据
这一步主要是读取数据,并进行必要的预处理。这里采用了tushare.pro的个股和指数日收益率数据,并对数据进行了适当的处理。
# 使用tushare获取数据
ts.set_token('your token')
pro = ts.pro_api()
# 获取沪深300与中国平安股票2018年全年以及2019年前7个交易日的日线数据
index_hs300 = pro.index_daily(ts_code='399300.SZ', start_date='20180101', end_date='20190110')
stock_000001 = pro.query('daily', ts_code='000001.SZ', start_date='20180101', end_date='20190110', fields='ts_code, trade_date ,pct_chg')
# 保留用于回归的数据,数据对齐
# join的inner参数用于剔除指数日线数据中中国平安无交易日的数据,比如停牌。
# 同时保留中国平安和指数的日收益率并分别命名两组列名y_stock, x_index,确定因变量和自变量
index_pct_chg = index_hs300.set_index('trade_date')['pct_chg']
stock_pct_chg = stock_000001.set_index('trade_date')['pct_chg']
df = pd.concat([stock_pct_chg, index_pct_chg], keys=['y_stock', 'x_index'], join='inner', axis=1, sort=True)
# 选中2018年的x,y数据作为现有数据进行线性回归
df_existing_data = df[df.index < '20190101']
# 注意:自变量x为pandas.DataFrame类型,其为二维数据结构,注意与因变量的pandas.Series数据结构的区别。也可以用numpy.array的.reshape((-1, 1))将数据结构改为二维数组。
x = df_existing_data[['x_index']]
y = df_existing_data['y_stock']经过简单处理,现在有了自变量x和因变量y。需要注意的是,sklearn.linear_model.LinearRegression类需要传入的自变量是一组二维数组结构,因此可以通过numpy的.reshape()方法将一维数组变更为二维数组,另一种方法就是使用pandas的DataFrame格式。
现在自变量和因变量看起来像这样:
print(x.head())
print(y.head())
x_index
trade_date
20180102 1.4028
20180103 0.5870
20180104 0.4237
20180105 0.2407
20180108 0.5173
trade_date
20180102 3.01
20180103 -2.70
20180104 -0.60
20180105 0.38
20180108 -2.56
Name: y_stock, dtype: float64可以通过.shape参数看到x有两个维度(243, 1),而y是一维数组,(243, )。
Step 3:建立模型并拟合数据
第三步,建立线性回归模型,并用中国平安和沪深300的2018年全年日线收益率数据进行拟合。先创建一个LinearRegression的实例用于建立回归模型:
model = LinearRegression()这里创建了一个默认参数的LinearRegression类实例。可以为LinearRegression传入以下几个可选参数:
fit_intercept:布尔值,默认为True。True为需要计算截距b0,False为不需要截距,即b0=0。
normalize:布尔值,默认为False。参数作用是将数据标准化,False表示不做标准化处理。
copy_x:布尔值,默认为True。True为保留x数组,False为覆盖原有的x数组。
n_jobs:整型或者None,默认为None。这个参数用于决定并行计算线程数。None表示单线程,-1表示使用所有线程。
模型建立以后,首先需要在模型上调用.fit()方法:
model.fit(x, y)用现有的数据集x-y,通过.fit()方法,可以计算出线性回归方程的最优权重b0和b1。换句话说,数据集x-y通过.fit()方法拟合了回归模型。.fit()方法输出self,也就是输出model模型本身。可以将以上两个语句简化为:
model = LinearRegression().fit(x, y)
Step 4:输出结果
数据拟合模型后,可以输出结果看看模型是否满意,以及是否可以合理的解释数据的趋势或者依赖关系。
可以通过调用.score()方法来获取model的R2:
model = LinearRegression().fit(x, y)
r_sq = model.score(x, y)
print('coefficient of determination: ', r_sq)
coefficient of determination: 0.5674052646582468同时,也可以通过调取model的.intercept_和.coef_属性获取截距b0和斜率b1:
print('intercept:', model.intercept_)
print('slope:', model.coef_)
intercept: 0.01762302497463801
slope: [1.18891167]需要注意的是,.intercept_是一个numpy.float64数值,而.coef_是一个numpy.array数组。
b0=0.017,表示自变量沪深300的日收益率为0时,因变量中国平安股票的日收益率大约为 0.017%。而b1=1.189,表示沪深300的日收益率增加1%时,中国平安股票的日收益率增加1.189%。反之亦然。
在上面的数据载入中,因变量y也可以是二维数组,这种情形下的输出结果和以上类似:
y = pd.DataFrame(y)
new_model = LinearRegression().fit(x, y)
print('intercept:', new_model.intercept_)
print('slope:', new_model.coef_)
intercept: [0.01762302]
slope: [[1.18891167]]可以看到此次输出结果中,b0变为一维numpy.array数组,而不是之前的float64数值。而b1输出一组二维numpy.array数组。
Step 5:模型预测
获得了比较合理的模型后,可以用现有数据或者新数据来进行预测。
本例中使用了沪深300指数2019年前7个交易日的收益率数据对中国平安股票进行预测,由于本文主旨是介绍线性回归的原理与相关使用方法,模型的预测效果本文中不做探讨。当然,也可以用2018年的现有的自变量数据获取回归模型的数据f(x)。
要获得预测结果,可以使用.predict()方法:
# 选2019年前7个交易日的数据作为新数据进行预测
df_new_data = df[df.index > '20190101']
# 将自变量x,数据类型为DataFrame
new_x = df_new_data[['x_index']]
# 预测
y_pred = model.predict(new_x)
print('predicted response:', y_pred, sep='\n')
predicted response:
[-1.60619253 -0.17022502 2.86601759 0.73929241 -0.23930079 1.21806713
-0.20601126].predict()方法需要将新的自变量传入该方法中以获得预测值。也可以用下面这种方法:
b0, b1 = model.intercept_, model.coef_
y_pred = b0 + b1 * new_x
y_pred.columns = ['y_pred']
print('predicted response:', y_pred, sep='\n')
predicted response:
y_pred
trade_date
20190102 -1.606193
20190103 -0.170225
20190104 2.866018
20190107 0.739292
20190108 -0.239301
20190109 1.218067
20190110 -0.206011这种方式可以将模型通过函数形式直观的表达出来。与.predict()的方法相比,这种方式的输出结果是一个DataFrame类型,其为二维数组结构。而.predict()仅输出一组一维numpy.array数组。
如果将new_x改为一维数组,y_pred的输出结果将与.predict()一致。
实践中,回归模型通常可以用来做预测。这意味着可以将一些新的自变量数据x传入拟合好的模型中来计算结果。比如假设一组沪深300日收益率数据[0, 1, 2, 3, 4],通过model获得中国平安股票的日收益率预测结果:
x_new = np.arange(5).reshape((-1, 1))
y_new = model.predict(x_new)
print(y_new)
[0.01762302 1.20653469 2.39544636 3.58435802 4.77326969]基于sklearn的多变量线性回归
多元线性回归和基础线性回归实现步骤基本一致。
Step 1:导入相关库和类
Step 2:读取数据
本例使用了tushare.pro中的沪深300作为因变量,中金的细分金融指数和细分有色指数作为两个自变量。
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
import tushare as ts
# 使用tushare获取数据
ts.set_token('your token')
pro = ts.pro_api()
# 获取沪深300,中金细分有色指数,中金细分金融指数2018年全年日线数据
index_hs300 = pro.index_daily(ts_code='399300.SZ', start_date='20180101', end_date='20190110')
index_metal = ts.pro_bar(ts_code='000811.CSI', freq='D', asset='I', start_date='20180101', end_date='20190110')
index_finance = ts.pro_bar(ts_code='000818.CSI', freq='D', asset='I', start_date='20180101', end_date='20190110')
# 保留用于回归的数据,数据对齐
# join的inner参数用于剔除指数日线数据中交易日不匹配的数据
# 同时保留三个指数的日收益率并分别命名两组列名y_zz300, x1_metal,x2_finance,确定因变量和自变量
index_hs300_pct_chg = index_hs300.set_index('trade_date')['pct_chg']
index_metal_pct_chg = index_metal.set_index('trade_date')['pct_chg']
index_finance_pct_chg = index_finance.set_index('trade_date')['pct_chg']
df = pd.concat([index_hs300_pct_chg, index_metal_pct_chg, index_finance_pct_chg], keys=['y_hs300', 'x1_metal', 'x2_finance'], join='inner', axis=1, sort=True)
# 选中2018年的x1,x2,y数据作为现有数据进行多变量线性回归
df_existing_data = df[df.index < '20190101']
# 提取多变量x1,x2,其数据类型为DataFrame。另外numpy需要的数据结构可以通过np.array(x)查看,也是二维数组。
x = df_existing_data[['x1_metal', 'x2_finance']]
y = df_existing_data['y_hs300']因变量和自变量如下
print(x.head())
print(y.head())
x1_metal x2_finance
trade_date
20180102 0.8574 1.6890
20180103 1.0870 -0.0458
20180104 0.9429 -0.3276
20180105 -0.7645 0.1391
20180108 2.2010 0.0529
trade_date
20180102 1.4028
20180103 0.5870
20180104 0.4237
20180105 0.2407
20180108 0.5173
Name: y_hs300, dtype: float64DataFrame类型可以非常直观的列出多个自变量,语法也相当简洁,最重要的是该数据类型可以直接应用于LinearRegression类。当然,这里也可以使用numpy.array的数据类型。
Step 3:建立模型并拟合数据
和前一个例子一样,建立模型并数据拟合:
model = LinearRegression().fit(x, y)Step 4:输出结果
一样的方式,通过model的.score(),.intercept_,.coef_属性获取回归模型的决定系数,截距b0,以及权重b1,b2:
model = LinearRegression().fit(x, y)
r_sq = model.score(x, y)
print('coefficient of determination:', r_sq)
print('intercept:', model.intercept_)
print('slope:', model.coef_)
coefficient of determination: 0.8923741832489497
intercept: 0.0005333314305123599
slope: [0.30529472 0.64221632]输出结果可以看出,截距b0大致为0,即当x1=x2=0时,f(x1, x2)=0。更多地,当x1增加1时,相应的f(x1, x2)增加大约0.305,而当x2增加1时,相应的f(x1, x2)增加大约0.642。反之亦然。
Step 5:模型预测
预测方式与前面也是一致的:
# 选中2019年前7个交易日的数据作为新数据进行预测
df_new_data = df[df.index > '20190101']
# 取自变量x1,x2
new_x = df_new_data[['x1_metal', 'x2_finance']]
# 预测
y_pred = model.predict(new_x)
print('predicted response:', y_pred, sep='\n')
predicted response:
[-1.4716842 1.17891556 2.55034238 0.17701977 -0.81283822 0.57159138
-0.19729323]也可以用下面这种方式:
y_pred = model.intercept_ + (model.coef_ * new_x).sum(axis=1)
print('predicted response:', y_pred, sep='\n')
predicted response:
trade_date
20190102 -1.471684
20190103 1.178916
20190104 2.550342
20190107 0.177020
20190108 -0.812838
20190109 0.571591
20190110 -0.197293
dtype: float64这种方式就是将每列自变量x1,x2乘上其对应的权重b1,b2,再加上一个固定的截距b0,得到预测的因变量。
基于sklearn的多项式回归
执行多项式回归步骤与前面也相似,只是需要增加一组经过转换的自变量作为非线性项,如x2。
Step 1:导入相关库和类
除了需要导入pandas和tushare,sklearn.linear_model.LinearRegression外,还需要导入sklearn.preprocessing中的PolynomialFeatures类用来处理非线性项。
import pandas as pd
import tushare as ts
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeaturesStep 2:读取数据
本例就采用tushare.pro上面的沪深300和中金细分金融指数数据。
# 获取沪深300,中金细分金融指数2018年全年日线数据及2019年前7个交易日数据
index_hs300 = pro.index_daily(ts_code='399300.SZ', start_date='20180101', end_date='20190110')
index_finance = ts.pro_bar(ts_code='000818.CSI', freq='D', asset='I', start_date='20180101', end_date='20190110')
index_hs300_pct_chg = index_hs300.set_index('trade_date')['pct_chg']
index_finance_pct_chg = index_finance.set_index('trade_date')['pct_chg']
df = pd.concat([index_hs300_pct_chg, index_finance_pct_chg], keys=['y_hs300', 'x_finance'], join='inner', axis=1, sort=True)
df_existing_data = df[df.index < '20190101']
x = df_existing_data[['x_finance']]
y = df_existing_data['y_hs300']Step 3:自变量转换
这个步骤是多项式回归需要执行的步骤。由于多项式回归中有x2项,因此需要将x数组转换成x2并作为新的列。
有很多种转换方式,比如使用numpy中的insert()方法,或者pandas的DataFrame添加x2列。本例中使用的是PolynomialFeatures类:
transformer = PolynomialFeatures(degree=2, include_bias=False)transformer是PolynomialFeatures类的实例,用于对自变量x进行转换。
PolynomialFeatures类中有以下几个可选参数:
degree:整型,默认为2。用于决定线性回归模型的阶数。
interaction_only:布尔值,默认为False。如果指定为True,那么就不会有xi2项,只有如xixj的交叉项。
include_bias:布尔值,默认为True。此参数决定是否将截距项添加为回归模型中的一项,即增加一列值为1的列。False表示不添加。
先将自变量x数据传入转换器transformer中:
transformer.fit(x)传入transformer之后,就可以使用.transform()方法获得转换后的数据x和x2:
x_ = transformer.transform(x)当然也可以用.fit_transform()来替代以上三个语句:
x_ = PolynomialFeatures(degree=2, include_bias=False).fit_transform(x)转换后的数组效果如下:
print(x_[:5])
[[ 1.6890000e+00 2.8527210e+00]
[-4.5800000e-02 2.0976400e-03]
[-3.2760000e-01 1.0732176e-01]
[ 1.3910000e-01 1.9348810e-02]
[ 5.2900000e-02 2.7984100e-03]]可以看到新的数据中有两列:一列是原始的自变量x的数据,另一列是x2项。
Step 4:建立模型并拟合数据
数据经过转换后,模型的建立和拟合的方式与前面一样:
model = LinearRegression().fit(x_, y)【注】模型中第一个参数变为经过处理后的数据x_,而不是原始的自变量x数组。
Step 5:输出结果
r_sq = model.score(x_, y)
print('coefficient of determination:', r_sq)
print('intercept:', model.intercept_)
print('coefficients:', model.coef_).score()返回R2=0.813,截距项b0大约为-0.014,x项的权重b1约为0.862,x2项的权重b2约为-0.014。
另外一种回归方法,也可以通过向转换器中传入不同的参数获得相同的回归结果:
x_ = PolynomialFeatures(degree=2, include_bias=True).fit_transform(x)这里将include_bias参数设置为True,其他的依然是默认参数。这种方法和step3中的相比,x_中会多出值为1的列,这列对应的是回归模型中的截距项:
print(x_[:5])
[[ 1.0000000e+00 1.6890000e+00 2.8527210e+00]
[ 1.0000000e+00 -4.5800000e-02 2.0976400e-03]
[ 1.0000000e+00 -3.2760000e-01 1.0732176e-01]
[ 1.0000000e+00 1.3910000e-01 1.9348810e-02]
[ 1.0000000e+00 5.2900000e-02 2.7984100e-03]]这组数据中,第一列全为1,第二列为x,第三列为x2。由于截距项已经包含在新的数据x_中了,因此在创建LinearRegression类时应该忽略截距项,即传入参数fit_intercept=False:
model = LinearRegression(fit_intercept=False).fit(x_, y)至此,模型和数据x_是匹配的。模型结果如下:
r_sq = model.score(x_, y)
print('coefficient of determination:', r_sq)
print('intercept:', model.intercept_)
print('coefficients:', model.coef_)
coefficient of determination: 0.8133705974408868
intercept: 0.0
coefficients: [-0.01395755 0.86215933 -0.01444605]可以看到.intercept_为0,但实际上截距b0已经包含在.coef_中了。其他结果都是一样的。
Step 6:模型预测
同样的,模型预测只需要调用.predict()方法,但是需要注意的是,传入的新数据也需要做转换:
# 选中2019年前7个交易日的数据作为新数据进行预测
df_new_data = df[df.index>'20190101']
# 取自变量x
new_x = df_new_data[['x_finance']]
# 自变量转换
new_x_ = PolynomialFeatures(degree=2, include_bias=True).fit_transform(new_x)
# 预测
y_pred = model.predict(new_x_)
print('predicted response:', y_pred, sep='\n')
predicted response:
[-1.32738808 0.98948547 2.38535216 -0.30448932 -0.40485458 0.78721444
-0.23448668]已经了解到了,多项式回归模型的预测方式与前面两例基本一样,只需要将用于预测的数据做下转换就好了。
如果有多个自变量,执行的过程也是一样的。这里使用了和前面提到的多变量回归中相同的三组指数日收益率数据:
x = df_existing_data[['x1_metal', 'x2_finance']]
y = df_existing_data['y_hs300']
# step3 数据转换
x_ = PolynomialFeatures(degree=2, include_bias=False).fit_transform(x)
# step4 建立模型并拟合数据
model = LinearRegression().fit(x_, y)
r_sq = model.score(x_, y)
intercept, coefficients = model.intercept_, model.coef_
# step5:模型预测
# 选中2019年前7个交易日的数据作为新数据进行预测
df_new_data = df[df.index > '20190101']
new_x = df_new_data[['x1_metal', 'x2_finance']]
# 自变量转换
new_x_ = PolynomialFeatures(degree=2, include_bias=False).fit_transform(new_x)
# 预测
y_pred = model.predict(new_x_)模型结果和预测如下:
print('coefficient of determination:', r_sq)
print('intercept:', intercept)
print('predicted response:', y_pred, sep='\n')
coefficient of determination: 0.8960573740272783
intercept: 0.020518382683722233
predicted response:
[-0.18180669 0.55726287 -0.79432939 0.17404118 2.57114362 1.23813068
-1.45582482]此结果的回归函数为f(x1, x2)=b0+b1x1+b2x2+b3x12+b4x1x2+b5x22。同时可以看到多项式回归的决定系数会高于多变量线性回归。决定系数R2高可能说明这是个不错的回归模型。
但是,在实践中,如此复杂的模型产生的高R2,也可能是过拟合导致的。如果想要检验回归模型的表现,需要使用新的数据测试模型,即用样本外的数据进行模型训练。
statsmodels库的线性回归应用
我们也可以使用statsmodels库实现线性回归,这个库的优点是可以输出回归模型更详细的结果。使用statsmodels的方法也和scikit-learn类似。
Step 1:导入相关库和类
import pandas as pd
import tushare as ts
import statsmodels.api as sm除了pandas,还需要导入statsmodels.api模块。
Step 2:输出结果
x = df_existing_data[['x1_metal', 'x2_finance']]
y = df_existing_data['y_hs300']如果用statsmodels计算截距,需要在x中添加全为1的列。statsmodels.api中有添加截距项的方法.add_constant(),该方法在数组中的第一列添加了值为1的列:
x = sm.add_constant(x)
print(x.head())
const x1_metal x2_finance
trade_date
20180102 1.0 0.8574 1.6890
20180103 1.0 1.0870 -0.0458
20180104 1.0 0.9429 -0.3276
20180105 1.0 -0.7645 0.1391
20180108 1.0 2.2010 0.0529修改后的x现在有三列,第一列是新的截距项,另外两列是原始数据。
Step 3:建立模型并拟合数据
回归模型是在statsmodels.regression.linear_model.OLS类建立的一个实例,OLS为最小二乘法:
model = sm.OLS(y, x)【注】.OLS()中第一个参数是因变量,后面一个是自变量。其中还有几个可选参数,可以参考statsmodels的官方文档。
模型建立后进行拟合:
results = model.fit()通过调用.fit(),可以获得模型结果results,results是statsmodels.regression.linear_model.RegressionResultsWrapper类的实例。模型结果中包含了大量关于这次回归模型的信息。
Step 4:获取结果
results中包含了回归模型的详细信息。提取结果的方法可以调用.summary():
print(results.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y_zz300 R-squared: 0.892
Model: OLS Adj. R-squared: 0.891
Method: Least Squares F-statistic: 995.0
Date: Sat, 20 Jul 2019 Prob (F-statistic): 6.76e-117
Time: 17:35:37 Log-Likelihood: -146.32
No. Observations: 243 AIC: 298.6
Df Residuals: 240 BIC: 309.1
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0005 0.029 0.019 0.985 -0.056 0.057
x1_metal 0.3053 0.023 13.385 0.000 0.260 0.350
x2_finance 0.6422 0.026 24.357 0.000 0.590 0.694
==============================================================================
Omnibus: 0.419 Durbin-Watson: 1.890
Prob(Omnibus): 0.811 Jarque-Bera (JB): 0.224
Skew: -0.055 Prob(JB): 0.894
Kurtosis: 3.101 Cond. No. 2.19
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.这张表提供的非常全面的回归结果。里面可以找到包括R2,b0,b1和b2在内的信息。同时也可以从上表中提取想要的值:
print('coefficient of determination:', results.rsquared)
print('adjusted coefficient of determination:', results.rsquared_adj)
print('regression coefficients:', results.params)
coefficient of determination: 0.8923741832489497
adjusted coefficient of determination: 0.8914773014426909
regression coefficients:
const 0.000533
x1_metal 0.305295
x2_finance 0.642216
dtype: float64以下是获取线性回归的属性的方法:
.rsquared:代表R2
.rsquared_adj:代表修正R2(经过自变量个数的调整后的R2)
.params:返回回归模型参数
可以对比scikit-learn中同类的回归模型,得到的模型结果都是一样的。
Step 5:预测模型
可以使用.fittedvalues或者.predict()方法获取模型产生的因变量f(x1,x2):
print('predicted response:', results.fittedvalues.head(), sep='\n')
predicted response:
trade_date
20180102 1.346996
20180103 0.302975
20180104 0.078006
20180105 -0.143532
20180108 0.706460
dtype: float64
print('predicted response:', results.predict(x.head()), sep='\n')
predicted response:
trade_date
20180102 1.346996
20180103 0.302975
20180104 0.078006
20180105 -0.143532
20180108 0.706460
dtype: float64或者使用新数据进行预测:
print('predicted response:', results.fittedvalues.head(), sep='\n')
# 选中2019年前7个交易日的数据作为新数据进行预测
df_new_data = df[df.index>'20190101']
# 取自变量x1,x2
new_x = df_new_data[['x1_metal', 'x2_finance']]
# 添加截距项
new_x = sm.add_constant(new_x)
# 预测
new_y = results.predict(new_x)
print(new_y)
trade_date
20190102 -1.471684
20190103 1.178916
20190104 2.550342
20190107 0.177020
20190108 -0.812838
20190109 0.571591
20190110 -0.197293
dtype: float64关于线性回归的不适用性情形
可以对比scikit-learn中同类的回归模型,得到的模型结果都是一样的。
在数据分析的过程中,有时线性回归并不适用,尤其是面对一些比较复杂的非线性模型时。线性回归不适用的时候,还有很多其他方法可以作为备选方案,比如支持向量机,决策树,随机森林以及神经网络。
这些方法都有Python库可用。而且大多数是免费开源的。这也是Python为什么是机器学习主要语言之一的原因。
而scikit-learn库也提供了除了线性回归以外的其他方法,而且用法和本文中的使用方法非常类似。该库包含了支持向量机,决策树,随机森林等等算法,这里不过多展开了。这些算法都可以通过.fit(),.predict(),.score()进行调用。
05
总结
本文介绍了什么是线性回归已经如何在Python中实现,可以利用pandas对数据进行处理,pandas直观高效的处理数据,并且可以与scikit-learn, statsmodels库实现无缝衔接。
线性回归可以通过两种方式实现:① scikit-learn:如果不需要回归模型的详细结果,用sklearn库是比较合适的。② statsmodels:用于获取回归模型详细统计结果。两个库都可以做进一步的探索。更详细的使用方法可以参考相关官方文档。
在Python中执行线性回归时,可以按照以下步骤执行:
① 导入需要的库和类。
② 提供数据,并且进行适当的预处理。
③ 创建回归模型,用现有数据进行拟合。
④ 检验模型是否合适,比如:欠拟合或者过拟合。
⑤ 应用模型进行预测。【参考链接】
https://realpython.com/linear-regression-in-python/【1】
https://sklearn.apachecn.org/#/【2】
