作者 | AI小昕
编辑 | 磐石
出品 | 磐创AI技术团队
【磐创AI导读】:本文详细介绍了神经网络在实战过程中的构建与调节方式。
之前我们讲了神经网络的起源、单层神经网络、多层神经网络的搭建过程、搭建时要注意到的具体问题、以及解决这些问题的具体方法。本文将通过一个经典的案例:MNIST手写数字识别,以代码的形式来为大家梳理一遍神经网络的整个过程。
一 、MNIST手写数字数据集介绍
MNIST手写数字数据集来源于是美国国家标准与技术研究所,是著名的公开数据集之一,通常这个数据集都会被作为深度学习的入门案例。数据集中的数字图片是由250个不同职业的人纯手写绘制,数据集获取的网址为:http://yann.lecun.com/exdb/mnist/。(下载后需解压)
具体来看,MNIST手写数字数据集包含有60000张图片作为训练集数据,10000张图片作为测试集数据,且每一个训练元素都是28*28像素的手写数字图片,每一张图片代表的是从0到9中的每个数字。该数据集样例如下图所示:

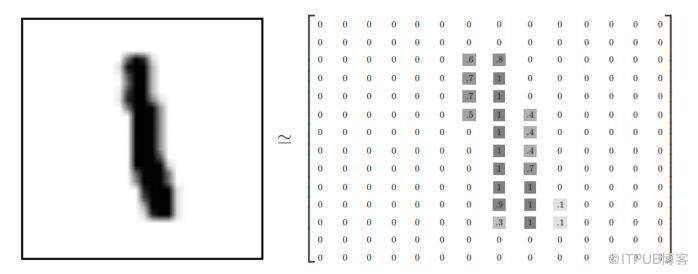
如果我们把每一张图片中的像素转换为向量,则得到长度为28*28=784的向量。因此我们可以把MNIST数据训练集看作是一个[60000,784]的张量,第一个维度表示图片的索引,第二个维度表示每张图片中的像素点。而图片里的每个像素点的值介于0-1之间。如下图所示:
此外,MNIST数据集的类标是介于0-9的数字,共10个类别。通常我们要用独热编码(One_Hot Encoding)的形式表示这些类标。所谓的独热编码,直观的讲就是用N个维度来对N个类别进行编码,并且对于每个类别,只有一个维度有效,记作数字1 ;其它维度均记作数字0。例如类标1表示为:([0,1,0,0,0,0,0,0,0,0]);同理标签2表示为:([0,0,1,0,0,0,0,0,0,0])。最后我们通过softmax函数输出的是每张图片属于10个类别的概率。
二 、网络结构的设计
接下来通过Tensorflow代码,实现MINIST手写数字识别的过程。首先,如程序1所示,我们导入程序所需要的库函数、数据集:
程序1:
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
接下来,我们读取MNIST数据集,并指定用one_hot的编码方式;然后定义batch_size、batch_num两个变量,分别代表一次性传入神经网络进行训练的批次大小,以及计算出训练的次数。如程序2所示:
程序2:
mnist_data=input_data.read_data_sets(“MNIST.data”,one_hot=True)
batch_size=100
batch_num=mnist_data.train.num_examples//batch_size
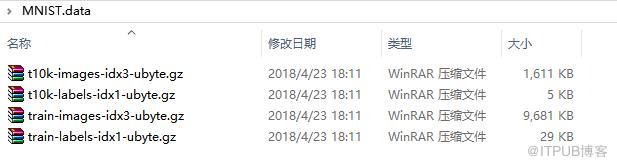
我们需要注意的是:在执行第一句命令时,就会从默认的地方下载MNIST数据集,下载下来的数据集会以压缩包的形式存到指定目录,如下图所示。这些数据分别代表了训练集、训练集标签、测试集、测试集标签。
接着我们定义两个placeholder,程序如下所示:
程序3:
x = tf.placeholder(tf.float32,[None,784])
y = tf.placeholder(tf.float32,[None,10])
其中,x代表训练数据,y代表标签。具体来看,我们会把训练集中的图片以batch_size批次大小,分批传入到第一个参数中(默认为None);X的第二个参数代表把图片转换为长度为784的向量;Y的第二个参数表示10个不同的类标。
接下来我们就可以开始构建一个简单的神经网络了,首先定义各层的权重w和偏执b。如程序4所示:
程序4:
weights = {
‘hidden_1’: tf.Variable(tf.random_normal([784, 256])),
‘out’: tf.Variable(tf.random_normal([256, 10]))
}
biases = {
‘b1’: tf.Variable(tf.random_normal([256])),
‘out’: tf.Variable(tf.random_normal([10]))
}
因为我们准备搭建一个含有一个隐藏层结构的神经网络(当然也可以搭建两个或是多个隐层的神经网络),所以先要设置其每层的w和b。如上程序所示,该隐藏层含有256个神经元。接着我们就可以开始搭建每一层神经网络了:
程序5:
def neural_network(x):
hidden_layer_1 = tf.add(tf.matmul(x, weights[‘hidden_1’]), biases[‘b1’])
out_layer = tf.matmul(hidden_layer_1, weights[‘out’]) + biases[‘out’]
return out_layer
如程序5所示,我们定义了一个含有一个隐藏层神经网络的函数neural_network,函数的返回值是输出层的输出结果。
接下来我们定义损失函数、优化器以及计算准确率的方法。
程序6:
#调用神经网络
result = neural_network(x)
#预测类别
prediction = tf.nn.softmax(result)
#平方差损失函数
loss = tf.reduce_mean(tf.square(y-prediction))
#梯度下降法
train_step = tf.train.GradientDescentOptimizer(0.2).minimize(loss)
#预测类标
correct_pred = tf.equal(tf.argmax(y,1),tf.argmax(prediction,1))
#计算准确率
accuracy = tf.reduce_mean(tf.cast(correct_pred,tf.float32))
#初始化变量
init = tf.global_variables_initializer()
如程序6所示:首先使用softmax函数对结果进行预测,然后选择平方差损失函数计算出loss,再使用梯度下降法的优化方法对loss进行最小化(梯度下降法的学习率设置为0.2)。接着使用argmax函数返回最大的值所在的位置,再使用equal函数与正确的类标进行比较,返回一个bool值,代表预测正确或错误的类标;最后使用cast函数把bool类型的预测结果转换为float类型(True转换为1,False转换为0),并对所有预测结果统计求平均值,算出最后的准确率。要注意:最后一定不要忘了对程序中的所有变量进行初始化。
最后一步,我们启动Tensorflow默认会话,执行上述过程。代码如下所示:
程序7:
step_num=400
with tf.Session() as sess:
sess.run(init)
for step in range(step_num+1):
for batch in range(batch_num):
batch_x,batch_y = mnist_data.train.next_batch(batch_size)
sess.run(train_step,feed_dict={x:batch_x,y:batch_y})
acc = sess.run(accuracy,feed_dict={x:mnist_data.test.images,y:mnist_data.test.labels})
print(“Step ” + str(step) + “,Training Accuracy “+ “{:.3f}” + str(acc))
print(“Finished!”)
上述程序定义了MNIST数据集的运行阶段,首先我们定义迭代的周期数,往往开始的时候准确率会随着迭代次数快速提高,但渐渐地随着迭代次数的增加,准确率提升的幅度会越来越小。而对于每一轮的迭代过程,我们用不同批次的图片进行训练,每次训练100张图片,每次训练的图片数据和对应的标签分别保存在 batch_x、batch_y中,接着再用run方法执行这个迭代过程,并使用feed_dict的字典结构填充每次的训练数据。循环往复上述过程,直到最后一轮的训练结束。
最后我们利用测试集的数据检验训练的准确率,feed_dict填充的数据分别是测试集的图片数据和测试集图片对应的标签。输出结果迭代次数和准确率,完成训练过程。我们截取400次的训练结果,如下图所示:

以上我们便完成了MNIST手写数字识别模型的训练,接下来可以从以下几方面对模型进行改良和优化,以提高模型的准确率。
首先,在计算损失函数时,可以选择交叉熵损失函数来代替平方差损失函数,通常在Tensorflow深度学习中,softmax_cross_entropy_with_logits函数会和softmax函数搭配使用,是因为交叉熵在面对多分类问题时,迭代过程中权值和偏置值的调整更加合理,模型收敛的速度更加快,训练的的效果也更加好。代码如下所示:
程序8:
#预测类别
prediction = tf.nn.softmax(result)
#交叉熵损失函数
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y,logits=prediction))
#梯度下降法
train_step = tf.train.GradientDescentOptimizer(0.2).minimize(loss)
#预测类标
correct_pred = tf.equal(tf.argmax(y,1),tf.argmax(prediction,1))
#计算准确率
accuracy = tf.reduce_mean(tf.cast(correct_pred,tf.float32))
如程序8所示:我们把两个参数:类标y以及模型的预测值prediction,传入到交叉熵损失函数softmax_cross_entropy_with_logits中,然后对函数的输出结果求平均值,再使用梯度下降法进行优化。最终的准确率如下图所示:
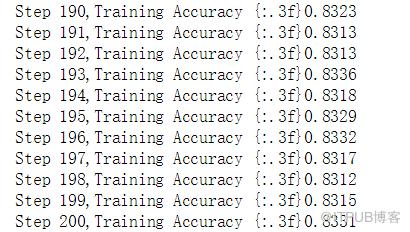
我们可以明显看到,使用交叉熵损失函数对于模型准确率的提高还是显而易见的,训练过程迭代200次的准确率已经超过了平方差损失函数迭代400次的准确率。
除了改变损失函数,我们还可以改变优化算法。例如使用adam优化算法代替随机梯度下降法,因为它的收敛速度要比随机梯度下降更快,这样也能够使准确率有所提高。如下程序所示,我们使用学习率为0.001的AdamOptimizer作为优化算法(其它部分不变):
程序9:
#Adam优化算法
train_step = tf.train.AdamOptimizer(1e-2).minimize(loss)
此外,如果你了解了过拟合的概念,那么很容易可以联想到测试集准确率不高的原因,可能是因为训练过程中发生了“过拟合”的现象。所以我们可以从防止过拟合的角度出发,提高模型的准确率。我们可以采用增加数据量或是增加正则化项的方式,来缓解过拟合。这里,我们为大家介绍dropout的方式是如何缓解过拟合的。
Dropout是在每次神经网络的训练过程中,使得部分神经元工作而另外一部分神经元不工作。而测试的时候激活所有神经元,用所有的神经元进行测试。这样便可以有效的缓解过拟合,提高模型的准确率。具体代码如下所示:
程序10:
def neural_network(x):
hidden_layer_1 = tf.add(tf.matmul(x, weights[‘hidden_1’]), biases[‘b1’])
L1 = tf.nn.tanh(hidden_layer_1)
dropout1 = tf.nn.dropout(L1,0.5)
out_layer = tf.matmul(dropout1, weights[‘out’]) + biases[‘out’]
return out_layer
如程序10所示,我们在隐藏层后接了dropout,随机关掉50%的神经元,最后的测试结果如下图所示,我们发现准确率取得了显著的提高,在神经网络结构中没有添加卷积层和池化层的情况下,准确率达到了92%以上。