这篇文章将看看北卡罗来纳州的研究三角背后的三角形使用数学的地理功能。
球面三角形
球面三角形是在球体表面绘制的三角形。它有三个顶点, 由球体上的点和三个边给出。三角形的边是在两个顶点之间运行的大圆圈的一部分。一个大圆是一个最大半径的圆, 一个与球体中心相同的圆。
球面几何的一个有趣的方面是, 三角形的边和角都是角度。由于球面三角形的两侧是圆弧, 因此它们具有角度度量, 即通过将每个顶点连接到球体中心而形成的角度。边线的弧长是其角度测量乘以球体半径的。
用a、 b和c表示这三个顶点。用a的对立面等表示。用α、β和γ分别表示 a、 b和c处的角度。
研究三角
研究三角是由杜克大学、北卡罗来纳州立大学和北卡罗来纳大学教堂山分校组成的 (球形!) 三角形。
(这就是这个名字的起源, 尽管现在它更宽松地应用于这三所大学周围的一般领域。
我们将把它作为我们的顶点
- a = unc 教堂山 (北纬 35.9046, 北纬 79 9.0468 w)
- b = 达勒姆杜克大学 (北纬 36.0011, 西华里78.9389),
- c = rateigh 的 ncsu (北纬 35.7872, 西华时78.6705)
数学
我们将使用与研究三角形相对应的球面三角形来说明 mathematica 的几个特征。
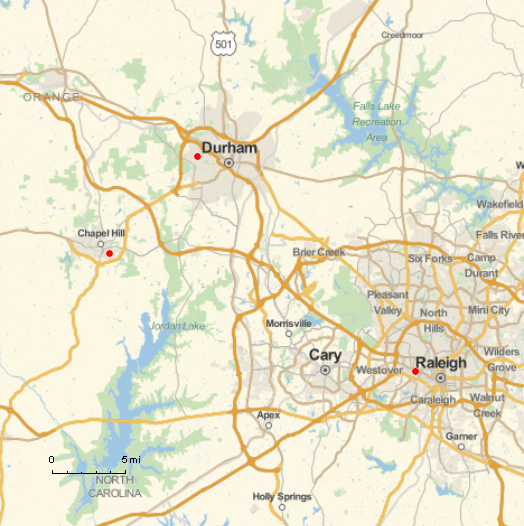
地图
上面的地图是用下面的数学代码制作的。
ptA = GeoPosition[{35.9046, -79.0468}]
ptB = GeoPosition[{36.0011, -78.9389}]
ptC = GeoPosition[{35.7872, -78.6705}]
GeoGraphics[{Red, PointSize[Large],
Point[ptA], Point[ptB], Point[ptC]},
GeoScaleBar -> "Imperial",
GeoRange -> 29000]请注意, 经度是东经, 所以上面的经度是负的。
距离
若要查找两个位置之间的距离, 可以使用 “cn/” 功能。例如:
GeoDistance[ptA, ptB]上面的代码告诉我, unc 和 duke 之间的距离是 8.99 185 英里。我假设它默认显示的是基于我在美国的位置的里程, 尽管上面的 < cn/> 选项默认为米。您可以使单位系统显式。例如:
GeoDistance[ptA, ptB, UnitSystem -> "Metric"]上述代码返回14.741 公里。
如果我们想找到以度为单位的边c的长度, 我们可以使用地球的半径。
r = PlanetData["Earth", "Radius"]
c = GeoDistance[ptA, ptB] 360 / (2 Pi r)这表明c为 0.130 014°。计算其他方面同样显示a = 0.30504°和b = 0.32739°。
角度
调用 < c\/> 返回 42.2432°, 这表明我们需要以大约42°的角度前进才能从 unc 步行到杜克大学。
的代码
GeoDirection[ptA, ptB] - GeoDirection[ptA, ptC]结果表明, 角度α为 68.668° (代码返回此角度的负值, 因为角度是顺时针的)。同样, 我们发现β = 87.98808°和γ = 23
这些角度加起来只有180°, 只是因为我们的三角形与地球总面积相比很小。实际和应该略超过180°, 但我们没有保留足够的精度来检测差异。一般来说, “球面过剩”, 即角度之和超过180°的量, 与三角形的面积成正比。
