在这篇文章中,我们将在实际方法中看到梯度下降和正常方程之间的实际差异。大多数新手机器学习爱好者在线性回归期间了解梯度下降,甚至不了解最被低估的法线方程,该方程远不复杂,为中小型数据集提供了非常好的结果。
如果你是机器学习的不熟悉者,或者不熟悉正常的方程或梯度下降,不要担心我会尽力用外行的术语来解释这些。因此,我首先要解释一下回归问题。
什么是线性回归?
它是入门级监督(给定功能和目标变量)机器学习算法。假设,我们在空间中绘制所有这些变量,然后这里的主要任务是拟合行,以最大限度地减少成本函数或损失(别担心,我也会解释这minimizes一点)。有各种类型的线性回归,如简单(一个特征)、多重和逻辑(用于分类)。本文考虑了多种线性回归。实际回归公式为:-
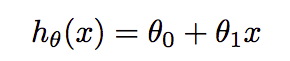
其中₀和₁是我们必须找到的参数,以最大限度地减少损失。在多重回归中,公式扩展为 α₀ =₁X₁ =2X2。成本函数发现算法实际值与预测值之间的误差相同的公式是:-
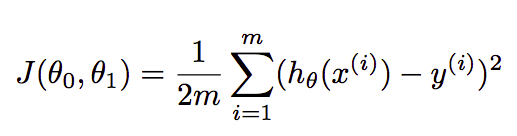
其中 m= 数据集中的示例或行数,xɪ ith 示例的要素值,yɪ ith 示例的实际结果。
梯度下降
它是一种优化技术,用于查找将成本函数降至最低的参数的最佳组合。在此,我们从参数的随机值(在大多数情况下为零)开始,然后不断更改参数以减少J(+₀,1₁)或成本函数,直到最终达到最小值。相同的公式是:-
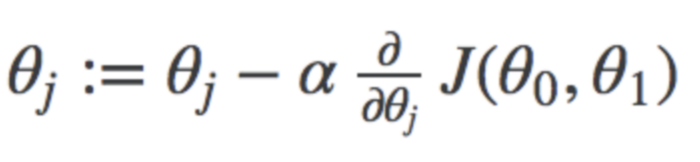
其中j表示否。参数的+ 表示学习速率。我不会深入讨论。你可以在这里找到这些手写笔记。
法线方程
在这种方法中,我们可以直接找到参数的最佳值,而无需使用梯度下降。当您使用较小的数据集时,它是一种非常有效的算法或不良的说oneline公式(因为它只包含一行)。
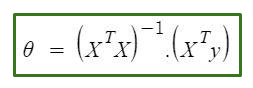
正常方程的唯一问题是,在大型数据集中查找矩阵的反比计算非常昂贵。
这是很多理论, 我知道, 但这是需要了解以下代码片段。而我只划伤了表面,所以请谷歌以上主题深入知识。
先决条件
我想你熟悉 python,已经在系统中安装了python 3您可以使用你喜欢的IDE。所有必需的图书馆都内置于阿纳康达套件中。
让我们的代码
我使用的数据集由3列组成,其中两列被视为要素,另一列被视为目标变量。数据集在GithHub 中可用。
首先,我们需要导入我们将在本研究中使用的库。在这里, numpy 用于创建用于训练和测试数据的NumPy数组, pandas 用于创建数据集的数据框并轻松检索值。用于绘制总体股票价格和预测 matplotlib.pyplot 价格等数据, mpl_toolkits 用于绘制3D数据, sklearn 用于拆分数据集和计算准确性。我们还导入 time 以计算每种算法所用的时间。
x
导入数字作为as np3从mpl_toolkitsimportmplot3d4导入matplotlib.pyplot作为plt5从sklearn。指标导入mean_squared_error6从sklearn。model_selection导入train_test_split7导入时间我们已将数据集加载到
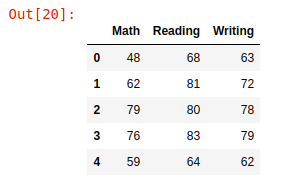
pandas数据框中,数据集的形状为(1000,3),然后只需打印前 5行,head()Python
x11dfpd.read_csv("学生.csv")23打印(df.形状)45头()
使用的数据集的预览
在这里,功能值即数学和读取保存在变量 X1 和 X2 中作为 NumPy 数组,而写入列被视为目标变量,其值保存在Y变量中。然后,我们绘制了此 3D 数据。
Python
x1