游戏理论与阿帕奇火花, 第4部分

系列如此之远

• 游戏理论与阿帕奇火花, 第1部分

• 游戏理论与阿帕奇火花, 第2部分

• 游戏理论与阿帕奇火花, 第3部分

将片断放在一起: 示例1

现在, 让我们重温上一篇文章中的示例 1, 并使用第1部分和第2部分算法来获取表3中的结果。我们从构造变量 < cn /和 < c2/

private static void Example1(){
    double cons_set1_vals[] = {0,8,4,2,8,4,2,8,4};
    DenseVector consSet1 = new DenseVector(cons_set1_vals);

    double u1_vals[] = {0,2,3,5,2,3,6,3,6};
    DenseVector u1 = new DenseVector(u1_vals);

    double cons_set2_vals[] = {4,4,0,0,8,6,0,4,2};
    DenseVector consSet2 = new DenseVector(cons_set2_vals);

    double u2_vals[] = {2,3,0,0,2,4,0,3,5};
    DenseVector u2 = new DenseVector(u2_vals);

    double cons_set3_vals[] = {1,2,4,2,4,2,1,8,4};
    DenseVector consSet3 = new DenseVector(cons_set3_vals);

    double u3_vals[] = {1,2,3,3,1,2,3,1,1};
    DenseVector u3 = new DenseVector(u3_vals);

    double cons_set4_vals[] = {2,1,0,0,2,1,0,1,0};
    DenseVector consSet4 = new DenseVector(cons_set4_vals);

    double u4_vals[] = {5,2,0,0,3,2,0,4,0};
    DenseVector u4 = new DenseVector(u4_vals);

    ArrayList<Vector> Ul = new ArrayList<Vector>();
    Ul.add(u1);
    Ul.add(u2);
    Ul.add(u3);
    Ul.add(u4);

    ArrayList<Vector> consumptionSets = new ArrayList<Vector>();
    consumptionSets.add(consSet1);
    consumptionSets.add(consSet2);
    consumptionSets.add(consSet3);
    consumptionSets.add(consSet4);
...

然后, 我们定义 s, 表1中的可用供应单位。

    double S_vals[] = {4,2,1,1,4,4,1,4,2};
    DenseVector S = new DenseVector(S_vals);
...

最后, 我们调用 < cn/ , 以获得最佳价格和相应的分配。然后, 我们将这些值传递给 < c/ /, 以获得与最优价格相对应的分配。

AssignmentsAndPrice Optimal = getOptimalAssignmentsAndPrice(Ul, S, 
    consumptionSets);
    getAllocations(Optimal.price, Ul, S, consumptionSets, Optimal.assignmentsL);
}

我们在 < cn/> 中的最后一个语句中放置了一个断点, 即返回分配的下一个语句, 以便通过调试器查看变量。这给了我们表3中的结果。

图 4.调试器中显示示例1的最佳价格和分配的变量。

将片断放在一起: 示例2

让我们重温上一篇文章中的示例 2, 并使用第1部分和第2部分算法来获取表5中的结果。我们从构造变量 < cn /和 < c2/> 开始, 这些变量对应于表4中每个代理1-4 中的行。

private static void Example2_Step1(){

    double cons_set1_vals[] = {50,20,30,100,0,0,0,0,0,0,0};
    DenseVector consSet1 = new DenseVector(cons_set1_vals);

    double u1_vals[] = {3,3,0,6,0,0,0,0,0,0,0};
    DenseVector u1 = new DenseVector(u1_vals);


    double cons_set2_vals[] = {40,40,20,50,0,0,0,0,0,0,0};
    DenseVector consSet2 = new DenseVector(cons_set2_vals);

    double u2_vals[] = {5,5,0,8,0,0,0,0,0,0,0};
    DenseVector u2 = new DenseVector(u2_vals);


    double cons_set3_vals[] = {0,0,0,0,20,20,10,50,0,0,0};
    DenseVector consSet3 = new DenseVector(cons_set3_vals);

    double u3_vals[] = {0,0,0,0,5,5,5,5,0,0,0};
    DenseVector u3 = new DenseVector(u3_vals);


    double cons_set4_vals[] = {0,0,50,0,80,30,40,50,100,100,50};
    DenseVector consSet4 = new DenseVector(cons_set4_vals);

    DenseVector u4 = (Vectors.zeros(11)).toDense();

    ArrayList<Vector> Ul = new ArrayList<Vector>();
    Ul.add(u1);
    Ul.add(u2);
    Ul.add(u3);
    Ul.add(u4);

    ArrayList<Vector> consumptionSets = new ArrayList<Vector>();
    consumptionSets.add(consSet1);
    consumptionSets.add(consSet2);
    consumptionSets.add(consSet3);
    consumptionSets.add(consSet4);
...

然后, 我们定义 s, 表4中的可用供应单位。

    double S_vals[] = {50,50,100, 50, 100, 50, 50, 100, 100, 100, 50};
    DenseVector S = new DenseVector(S_vals);
...

最后, 我们调用 < cn/ , 以获得最佳价格和相应的分配。然后, 我们将这些值传递给 < c/ /, 以获得与最优价格相对应的分配。

    AssignmentsAndPrice Optimal = getOptimalAssignmentsAndPrice(Ul, S,
       consumptionSets);
    getAllocations(Optimal.price, Ul, S, consumptionSets, Optimal.assignmentsL);
}

我们在 < cn/> 中的最后一个语句中放置了一个断点,即返回分配的下一个语句, 以便通过调试器查看变量。这显示了下面的结果表5。

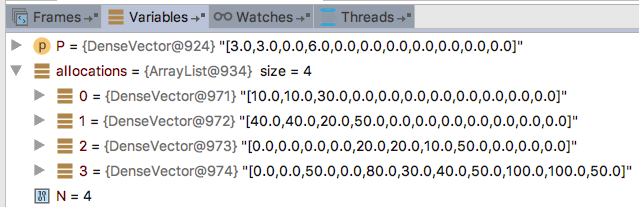
图 5.调试器中显示示例2步骤1的最佳价格和分配的变量。

货物的运输是根据上述分配来实现下图中概述的状态, 即通过每个环节运输的货物数量以红色突出显示”类 =” fr-fref-dib “src=”http://www.cheeli.com.cn/wp-content/uploads/2018/11/10626720-alloc2.png “标题 =” 步骤1完成后的货物运输 “width=”829″/>

图 6.步骤1完成后的货物运输。(从图2复制。

对于步骤 2, 创建了一个新的配方, 如下所示。对于代理 2, 每个运输链路的值大于代理1、3的值, 因为 b 类货物的运输具有更高的优先级 (5 vs 4)。

资源类型	1	2	3个	4个	5	6	7。	8	9	10	11
描述	链接 1-3	链接 1-4	链接 1-5	链接 1-6	链接 2-3	链接 2-4	链接 2-5	链接 2-6	链接 3-6	链接 4-6	链接 5-6
s	50	50	100元	50	100元	50	50	100元	100元	100元	50
代理 1 (a)
美国	0	0	4个	4个	0	0	0	0	4个	4个	4个
我	0	0	100元	50	0	0	0	0	10	10	30
代理 2 (b)
美国	0	0	0	0	0	0	0	0	5	5	5
我	0	0	0	0	0	0	0	0	40	40	20
代理 3 (c)
美国	0	0	0	0	0	0	0	0	4个	4个	4个
我	0	0	0	0	0	0	0	0	20	20	10
代理 4 (辅助)
美国	0	0	0	0	0	0	0	0	0	0	0
我	50	50	0	0	100元	50	50	100元	30	30	0

表7。

就我们的代码而言, 表7中的信息的使用与上一步相似。

private static void Example2_Step2(){

    double cons_set1_vals[] = {0,0,100, 50,0,0,0,0,10,10,30};
    DenseVector consSet1 = new DenseVector(cons_set1_vals);

    double u1_vals[] = {0,0,4,4,0,0,0,0,4,4,4};
    DenseVector u1 = new DenseVector(u1_vals);


    double cons_set2_vals[] = {0,0,0,0,0,0,0,0,40,40,20};
    DenseVector consSet2 = new DenseVector(cons_set2_vals);

    double u2_vals[] = {0,0,0,0,0,0,0,0,5,5,5};
    DenseVector u2 = new DenseVector(u2_vals);


    double cons_set3_vals[] = {0,0,0,0,0,0,0,0,20,20,10};
    DenseVector consSet3 = new DenseVector(cons_set3_vals);

    double u3_vals[] = {0,0,0,0,0,0,0,0,4,4,4};
    DenseVector u3 = new DenseVector(u3_vals);


    double cons_set4_vals[] = {50,50,0,0,100,50,50,100,30,30,0};
    DenseVector consSet4 = new DenseVector(cons_set4_vals);

    DenseVector u4 = (Vectors

密度 ();

arraylist & lt; vector & gt; ul = 新 arraylist & lt; vector & gt; ();
Ul.add(u1);
Ul.add(u2);
Ul.add(u3);
Ul.add(u4);

arraylist & lt; vector & gt; 消费集 = 新 arraylist & lt; 矢量 & gt; ();
consumptionSets.add(consSet1);
consumptionSets.add(consSet2);
consumptionSets.add(consSet3);
consumptionSets.add(consSet4);

双 s _ val [] = {50, 50100, 50100, 50, 50100100, 50};
拒绝向量 s = 新的登塞向量 (s _ val);

分配—————————————————————————————-
分配 (最优价格, ul, s, 消费集, 最优. 分配 l);

}

调试点向我们显示了最终结果, 如下所示。

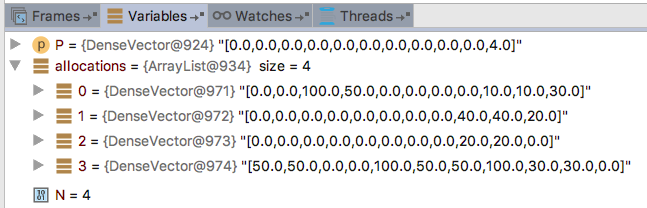
图 7.调试器中显示示例2步骤2的最佳价格和分配的变量。

因此, 该算法产生以下最优价格和分配。

资源类型	1	2	3个	4个	5	6	7。	8	9	10	11
描述	链接 1-3	链接 1-4	链接 1-5	链接 1-6	链接 2-3	链接 2-4	链接 2-5	链接 2-6	链接 3-6	链接 4-6	链接 5-6
价格	0	0	0	0	0	0	0	0	0	0	4个
代理 1 (a)	0	0	100元	50	0	0	0	0	10	10	30
代理 2 (b)	0	0	0	0	0	0	0	0	40	40	20
代理 3 (c)	0	0	0	0	0	0	0	0	20	20	0
代理 4 (辅助)	50	50	0	0	100元	50	50	100元	30	30	0

表8。

货物的运输是根据上述分配来实现下图中概述的状态, 即通过每个环节运输的货物数量以红色突出显示。

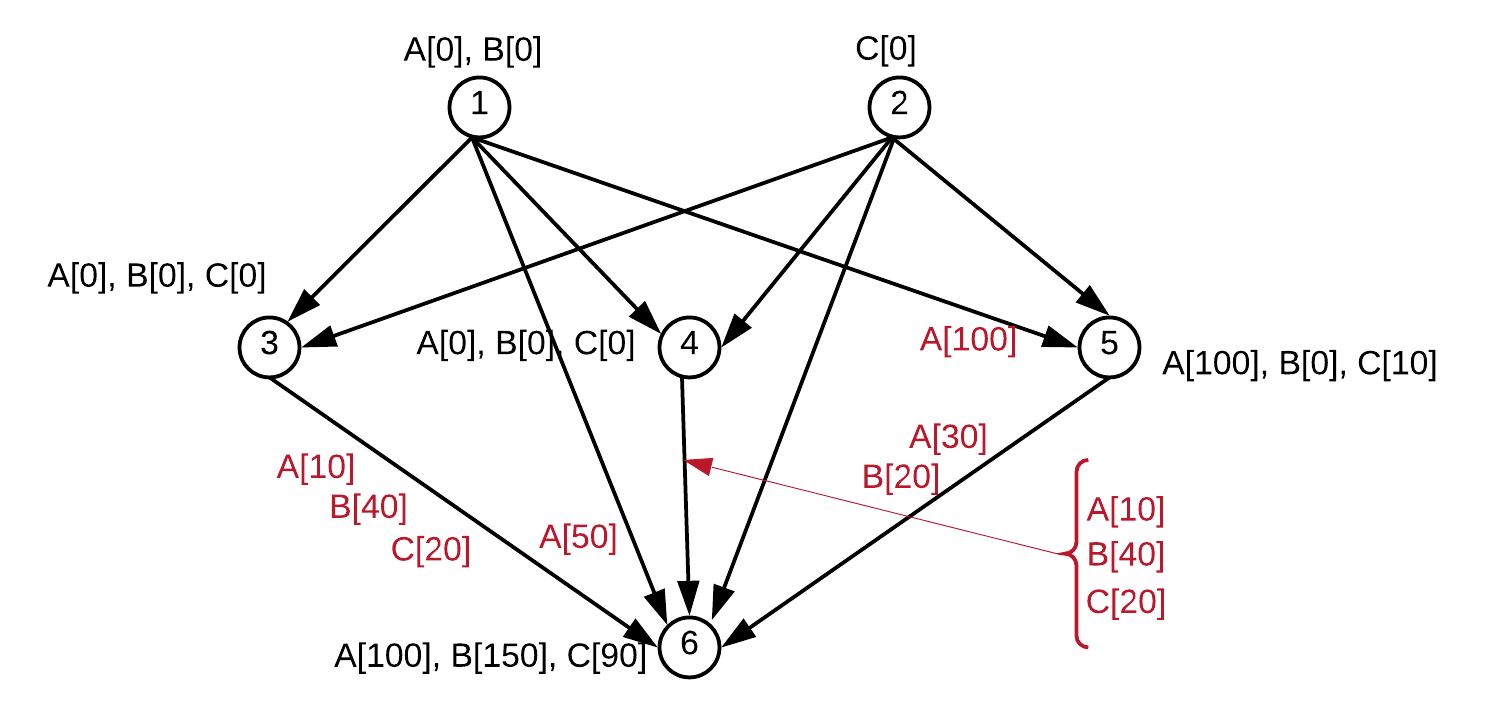
图 8.步骤2后的货物运输完成。

此时, 所有 b 型货物都已运输这些步骤 (3-5) 如下所示 (为了简单起见, 我们省略了编码细节, 因为这些步骤与上面的代码类似)。

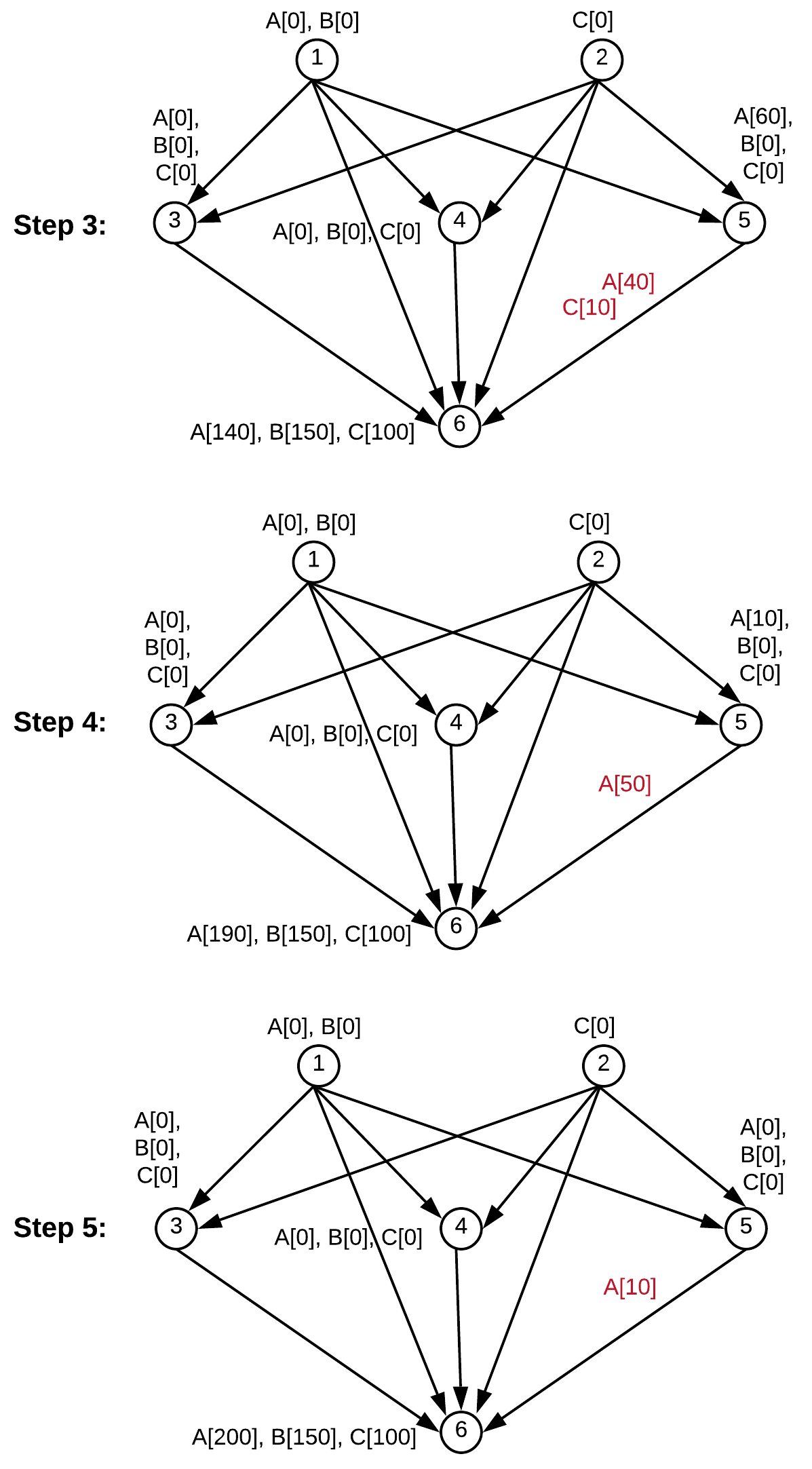
图 9.步骤3-5 之后的货物运输已经完成。

结论

本文讨论了一种基于博弈论的资源优化分配算法。该算法提供了一种基于公平的平衡, 即每个代理 (投标人) 最大化其效用, 而资源管理器 (拍卖师) 将其分配的资源的价格最大化。此外, 所有可用的单位都分配给所有资源类型, 没有代理被迫接受超出其意愿的任何内容。该算法是基于经济学家奥苏贝尔的高效动态拍卖方法。

通过两个实例表明, 该算法可以应用于不同类型的资源分配问题。在一个例子中, 我们应用该算法将云计算资源 (如 cpu、内存、带宽) 分配给计算客户端。其次, 将该算法应用于物流实例, 在该实例中, 各类货物都是通过共享运输资源运输的。

我们提供了一个使用 apache spark 机器学习库的算法实现, 并回顾了相应的 java 代码。apache spark 机器学习库对于实现该算法特别有用, 因为相应的 java api 具有内置的矢量操作, 这对于执行算法至关重要。

在各方面, 奥苏贝尔原纸中的动态拍卖方法比我们在本文中考虑的版本更广泛。首先, 在本文中, 我们将值函数 u_i(x) 限制为 x 上的线性函数。但是, 原始算法没有此限制。相反, 允许更广泛的凹函数类。我们的限制是为了简单起见, 但我们也认为线性值函数仍然是非常有效的, 在许多实际应用 (感兴趣的用户可以参考这篇文章的各种凹函数, 可以作为一个值函数在原纸)。其次, 寻找最优价格的原始算法不一定从0的初始价格向量开始。然而, 为了处理不同于0的初始价格向量, 该算法有一个降序截面和一个上升部分, 因此它更加复杂。通过将初始价格向量限制为 0, 我们的实现变得更简单。第三, 为了实现一致性, 我们将算法分为第1部分和第2部分。虽然这些概念是固有的, 但原始算法并没有以这种方式进行显式的分离。konur unyelioglu