从 dijkstra 到 a 星 (a *), 第1部分: dijkstra 算法

查找从一个节点到另一个节点的路径是一个经典的图形搜索问题, 我们可以使用多个遍历算法 (如bfs或dfs)来解决此问题。但是, 如果我们想要找到从一个节点到另一个节点的最短路径, bfs或dfs遍历不会对我们有太大帮助, 因此我们需要使用其他算法, 如bellman-ford、 floyd-warshall 或 dijkstra。在本文中, 我想重点介绍 dijkstra 算法, 并了解我们可以做些什么来改进它, 使它更快, 从而将它转换为 a 星 (a *) 算法。

在正加权图中寻找最短路径

在正加权图中, 我们可以使用dijkstra算法计算从a点到b 点成本最低的路径。如果有负成本的路径, dijkstra 就行不通了, 所以我们必须寻找其他方法, 比如bellman-ford或活期-warshall算法。

该算法的主要思想是, 从一个节点开始, 下一个要访问的节点是从源到它的遍历成本最低的节点。因此, 这看起来几乎像bfs, 通过有一个带有节点的队列, 并且在每次迭代中, 我们都会从队列中提取一个元素并访问它。dijkstra和bfs之间的区别在于, 使用bfs , 我们有一个简单的fifo队列, 下一个要访问的节点是在队列中添加的第一个节点。但是, 使用dijkstra,我们需要以迄今为止最低的成本拉节点。

让我们看一个简单的例子:

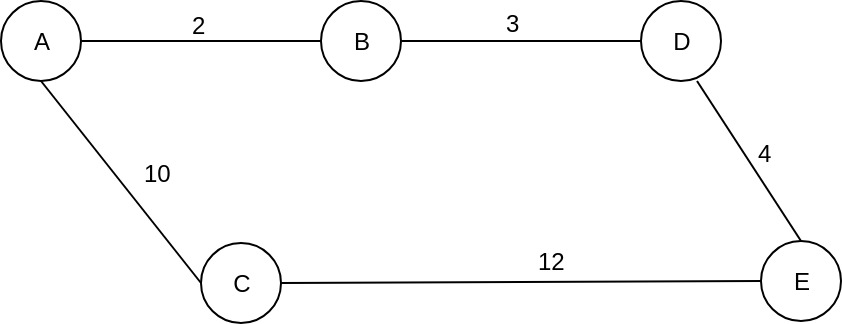
我们希望使用bfs从a到e , 因此, 我们将使用一个简单的 fifo 队列。从节点a开始, 我们得到相邻的节点b和c, 并将它们放在队列中。接下来, 我们从队列中提取已添加的第一个元素节点 b, 并检查相邻节点 a 和d. a被访问, 所以我们忽略了它, 我们将节点d添加到队列中。因此, 队列现在包含节点c和d。

我们向前移动, 并从队列中获取节点c , 检查相邻节点, a和e.我们忽略了 a , 因为我们已经访问过它, 我们看到我们到达了 e , 我们停了下来。因此, 我们找到了一条路径, a > c > e,总成本为22。这就是成本最低的道路吗？好吧, 不。让我们通过更改从队列中检索元素的方式来更改算法以查找最短路径。

作为一个小观察, 经典的 bfs算法遍历所有图形, 当队列为空时, 它就会停止。这是一个稍有变化的算法, 更贪婪, 当我们找到目的地时, 我们就会停下来。

因此, 让我们看看我们得到了什么, 如果我们从队列中提取到目前为止成本最低的节点。从a 开始, 我们检查相邻节点 b 和 c, 并计算从a 到每个节点的路径成本。因此, 我们有一个队列与:

Queue: {
  B, cost_so_far: 2
  C, cost_so_far: 10 
}

现在, 使用dijkstra,我们选择访问具有最低的节点 cost_so_far , 即bcost_so_far节点 d 是 b 加上 b 和 d 之间的成本, 即 3. cost_so_far 所以我们的总成本是5。我们把它放在队列中, 队列将如下所示:

Queue {
  C, cost_so_far: 10,
  D, cost_so_far: 5
}

在相同的过程之后, 我们从队列中提取节点d , 因为它的节点 cost_so_far 最少, 尽管以前添加了c 。我们检查它, 我们看到我们达到e cost_so_far 等于 10 + 4 = 14。我们将其添加到队列中, 再次从队列中选择要访问的下一个节点。队列将如下所示:

Queue {
  E, cost_so_far: 14
  C, cost_so far: 10
}

我们不会停在这里, 但我稍后会解释。但是, 就目前而言, 让我们继续这一进程。我们看队列, 我们拉的节点是最低 cost_so_far 的, 即c。c有两个邻居, a以前访问过, e cost_so_far 等于14。现在, 如果我们计算到e的路径成本, 通过c, 我们将有一个 cost_so_far 等于 22, 这大于当前 cost_so_far 的 14, 所以我们不会改变它。

向前移动, 我们将有一个具有单个节点 e 的队列。我们拿着它, 看到我们到达了目的地, 所以我们停下来了。我们现在的路径成本最低, 从a到e, a-> b-> > e,总成本为14。因此, 使用bfs我们找到了一条总成本为22的路径, 但是, 使用dijkstra, 我们看到了一条成本更低的路径, 成本更低, 为14。

那么, 为什么我们第一次到达节点e时没有早点停下来呢？好吧, 让我们把e和d之间的边缘成本更改为20。

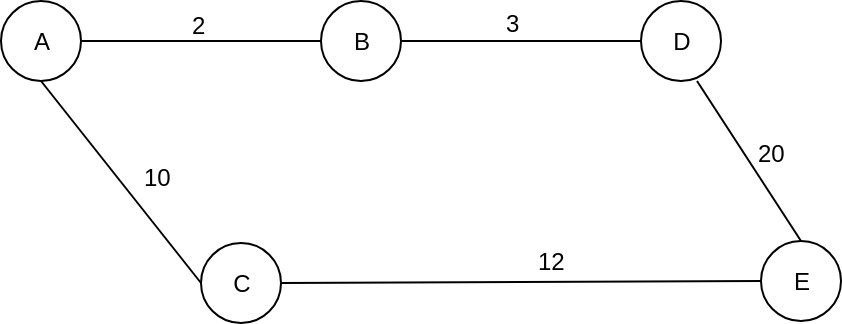
在这种情况下, 从a到d的所有步骤都是相同的。但是, 在我们访问节点 d 后, 队列将如下所示:

Queue {
  E, cost_so_far: 25
  C, cost_so far: 10
}

我们采用c, 因为它有最低 cost_so_far 的, 我们计算 cost_so_far e到c的潜力, 这是 22, 我们看到新的值低于当前 cost_so_far , 25。所以我们更新它, e将有一个 cost_so_far 新的等于 22, 通过c。当我们从队列中提取节点e时, 我们看到我们到达了目的地, 我们找到了从a到e成本最低的路径, 即a-> c-> e,总成本为22。

因此, 即使我们访问一个节点时, 我们 “看到” 我们的目标, 我们计算 cost_so_far 它, 我们不会停在那里, 因为可能有另一条路径具有更低的成本。所以, 每次访问一个节点, 我们都会看它的邻居, 即使 cost_so_far 我们在以前访问另一个节点时已经计算出了 a, 我们也会通过更新 cost_so_far 是否比当前节点低来检查是否找到了更好的路径

迪伊克斯特拉实施建议

让我们看看如何实现这一点。我们将从一个节点开始, 该节点的邻居有一个名称和一个邻接列表。除了这些字段, 我们还可以添加一个 cost_so_far 字段, 让我们称之为 g_cost 字段, 以及一个父字段。搜索算法将设置这两个字段, 我们将使用它们来查找从一个节点到另一个节点的成本最低的路径。我们可以通过将 “无限 g_cost ” 和 “父” 设置为 “无限 null ” 来初始化这些字段。这可能如下所示:

static class Node{
  public final String name;
  public List<Edge> adjacency = new ArrayList<>();
  public Node parent;
  public double g_cost = Integer.MAX_VALUE;

  public Node(String name){
    this.name = name;
  }

  public void addNeighbour(Node neighbour, int cost) {
    Edge edge = new Edge(neighbour, cost);
    adjacency.add(edge);
  }

  public String toString(){
    return name;
  }
}

边具有成本和目标节点。

static class Edge{
  public final double cost;
  public final Node target;

  public Edge(Node target, double cost){
    this.target = target;
    this.cost = cost;
  }
}

现在的算法。正如我之前所说, 此算法的主要思想是, 从一个节点开始, 要访问的下一个节点是一个从源到它的成本最低的节点。为此, 我们可以使用“优先级队列“, 让我们将其称为 “边框”, 节点按. g_cost当我们访问一个节点时, 如果我们为它的邻居找到更好的方法, 我们只需将它们添加到边框 g_cost 中并更新, 而且, 由于边界是优先级队列, 它将维护按值排序的节点 g_cost 。当我们访问目的地时, 这意味着我们找到了从源头到目的地的最佳路径, 我们就停下来了。

这是算法实现:

public static void dijkstraSearch(Node source, Node destination) {
  source.g_cost = 0;

  PriorityQueue<Node> frontier = new PriorityQueue<>(new Comparator<Node>() {
    @Override
    public int compare(Node o1, Node o2) {
      return Double.compare(o1.g_cost, o2.g_cost);
    }
  });


  frontier.add(source);

  int numberOfSteps = 0;
  while (!frontier.isEmpty()) {
    numberOfSteps++;
    // get the node with minimum g_cost
    Node current = frontier.poll();

    System.out.println("Current node: " + current.name);

    // we have found the destination
    if (current.name.equals(destination.name)) {
      break;
    }

    // check all the neighbours
    for (Edge edge: current.adjacency) {

      Node neigh = edge.target;
      double cost = edge.cost;

      double newCost = current.g_cost + cost;

      if (newCost < neigh.g_cost) {
        neigh.parent = current;
        neigh.g_cost = newCost;

        // reset frontier order
        if (frontier.contains(neigh)) {
          frontier.remove(neigh);
        }

        frontier.add(neigh);
      }
    }
  }

  System.out.println("Number of steps: " + numberOfSteps);
}

同样, 正如我之前对bfs 实现所说的, 这是 dijkstra 算法的一个稍微修改的版本, 称为统一成本搜索, 当我们找到目标时, 我们会在该算法中停止。经典的 dijkstra算法继续访问所有节点, 直到队列为空, 找到从起始节点到所有其他节点的最小路径成本。

让我们看看这是如何在真正的地图上工作的假设我们要在最短的路径上从阿拉德开车到布加勒斯特。

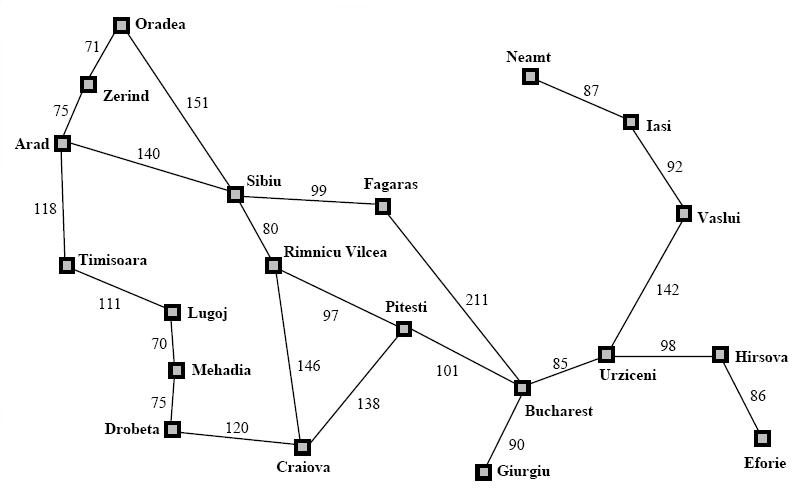
我们可以看到, 我们可以走多条路线。我们可以从阿拉德到蒂米什瓦拉, 然后卢戈杰, 等等, 或者我们可以选择锡比乌, 然后法加拉, 直接去布加勒斯特。但我们不知道哪条路的成本最低。所以, 这是一个很好的候选人的 dijkstra算法。在罗马尼亚地图上运行我们的实现将得到这样的:

Total Cost: 418.0
Path: [Arad, Sibiu, Rimnicu Vilcea, Pitesti, Bucharest]

这就是成本最低的道路 (相信我, 我其实来自罗马尼亚, 我可以向你保证, 这是最短的路)。因此, 使用 dijkstra 算法, 我们能够找到成本最低的路径, 但让我们看看在访问节点时打印节点所需的步骤是多少:

Current node: Arad
Current node: Zerind
Current node: Timisoara
Current node: Sibiu
Current node: Oradea
Current node: Rimnicu Vilcea
Current node: Lugoj
Current node: Fagaras
Current node: Mehadia
Current node: Pitesti
Current node: Craiova
Current node: Drobeta
Current node: Bucharest
Number of steps: 13

因此, 我们需要访问13个节点, 以找到最佳路径。正如你所看到的, 从阿拉德我们没有直接去锡比乌, 我们是通过泽林到达的, 然后是蒂米什瓦拉, 然后是锡比乌。而且, 即使在那之后, 我们也没有去里姆尼库瓦尔塞亚, 而是去了奥拉迪亚, 因为那是迄今为止成本最低的节点。这就是这个算法的工作原理。13个节点访问, 以找到我们的路径, 其中许多节点没有在路径上的成本最低反正。但我们不知道这一点, 我们不得不去看望他们才能知道。

这都是第1部分!来 abc 周一, 当我们将涵盖如何使用 a 星 [a (*)] 算法解决这个问题。