在生成人工智能、数据科学、机器学习和分析的多层面世界中,了解数据点之间的距离和关系至关重要。这就是大型语言模型 (LLM) 理解上下文和检索数据的方式。大量非结构化数据可以轻松存储在以三维空间表示的矢量数据库中。
每当用户提出查询时,都会从数据库中检索最近似的答案。看到数据如何存储以及该计算如何检索特定信息是令人惊奇的。
有许多高级方法可以计算向量之间的距离。在本文中,我们将探讨一些重要的距离度量,例如曼哈顿距离、欧几里德距离、余弦距离和点积。
机器学习背景下的向量是什么?
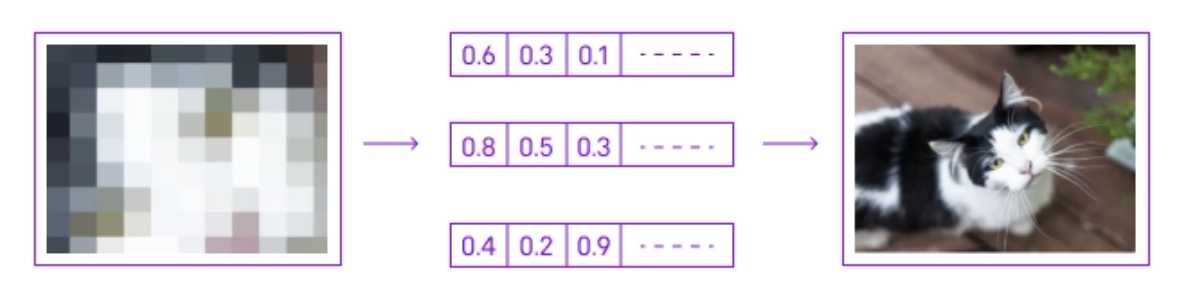
在生成人工智能领域,向量作为表示和操作复杂数据的手段发挥着至关重要的作用。在这种情况下,向量通常是编码大量信息的高维数字数组。例如,在图像生成的情况下,每个图像可以转换为表示其像素值的向量或通过深度学习模型提取的更抽象的特征。
这些向量成为人工智能算法理解和生成新内容的语言。通过在多维空间中导航和修改这些向量,生成式人工智能可以生成新的合成数据实例(无论是图像、声音还是文本),从而模仿原始数据集的特征。这种矢量操作是人工智能从数据中学习并根据学习生成实际输出的能力的核心。
什么是矢量相似性搜索?
查询涉及在高维空间中查找给定向量的最近邻居。此过程称为向量相似度搜索或近似最近邻 (ANN) 搜索,查找与查询向量的距离(例如,欧几里得距离或余弦相似度)最接近的向量。该方法捕获不同数据点之间上下文或特征的相似性,这对于推荐系统、相似性搜索和聚类等任务至关重要。
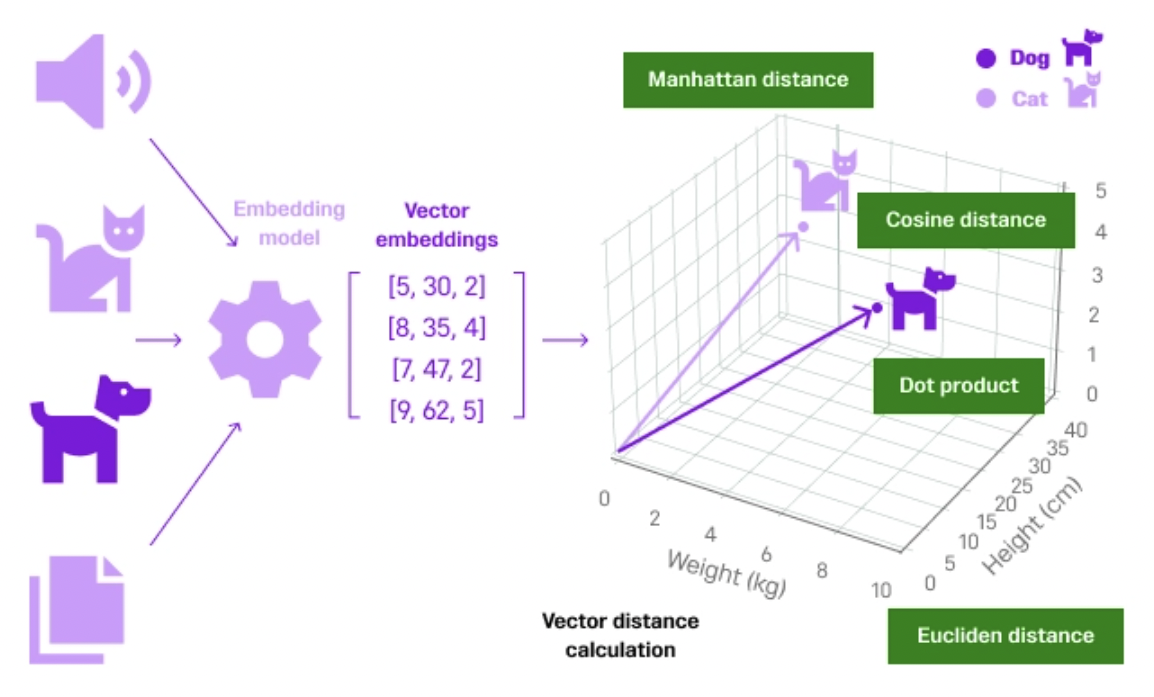
考虑来自各种来源的非结构化数据,如上图所示。数据通过嵌入模型(来自 OpenAI、Cohere、HuggingFace 等)将内容转换为小词块(向量嵌入)。每个词块都被分配一个数值,这个过程称为标记化。创建矢量嵌入后,它们会在矢量数据库内的三维空间中表示,所有矢量数据都存储在其中。
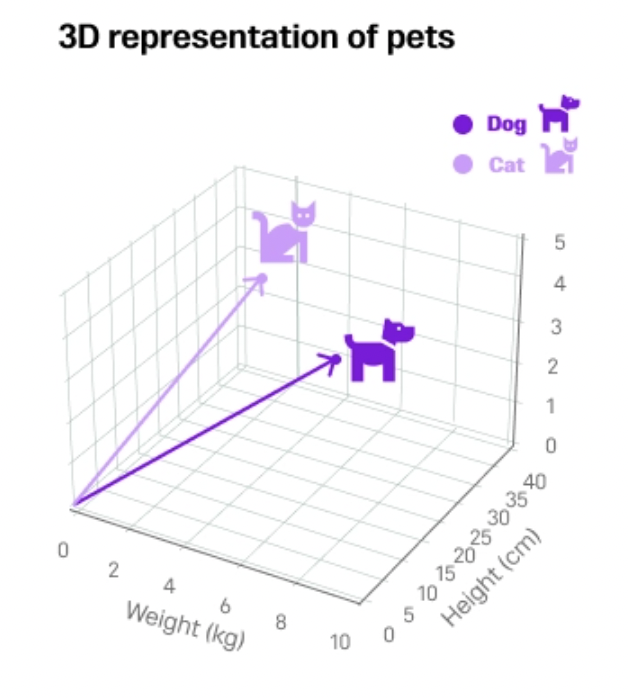
在我们的例子中,如上图所示,非结构化数据“猫”和“狗”首先被转换为矢量数据,然后在彼此更接近的三维空间中表示,因为它们都属于相同的宠物类别。如果我们再考虑一个“汽车”的例子,那么它的表示方式就与“猫”和“狗”相距甚远,因为它不属于宠物类别。
通过这种方式,相似的对象被放置在一起,当用户查询进入时,系统会考虑上下文,并将更相似的对象检索回给用户。
矢量相似度搜索是如何计算的
有不同的技术来计算向量之间的距离。点积、欧几里德距离、曼哈顿距离和余弦距离都是矢量相似性搜索中使用的基本概念。每一个都衡量多维空间中两个向量之间的相似性。
曼哈顿距离

曼哈顿距离是一种通过对两点(向量)坐标的绝对差求和来计算两点(向量)之间距离的方法。想象一下在一个完美网格布局的城市中航行:两点之间的曼哈顿距离是您必须垂直和水平移动才能从一个点到达另一个点而无需走对角捷径的街区总数。在向量的上下文中,它是相似的:通过将向量的每个相应分量的绝对差相加来计算距离。
欧几里德距离

欧几里得距离,通常称为 L2 范数,是测量两个点或向量之间距离的最直接方法,类似于我们通常思考物理世界中距离的方式。想象一下在地图上的两点之间画一条直线;欧几里德距离是这条线的长度。
该指标广泛应用于许多领域,包括用于测量实际距离的物理学、用于聚类和分类等任务的机器学习算法,以及在需要确定直接距离或直线距离的日常场景中。它与我们对距离的直观理解自然一致,使其成为数据分析和几何的基本工具。
余弦距离

余弦距离是两个非零向量之间相似性的度量,用于评估它们之间角度的余弦。它不是传统意义上的“距离”,而是确定向量相对于彼此如何定向的度量,无论其大小如何。想象两个箭头从同一点出发;它们之间的角度越小,它们在方向上越相似。
此度量在文本分析和信息检索等领域特别有用,其中向量的方向(例如表示高维空间中的文档或查询)比它们的绝对位置或大小更重要。
点积

点积捕获两个向量之间的关系。想象两个箭头从同一个起点延伸;点积量化了一个箭头与另一个箭头的方向对齐的程度。从数学上讲,它是通过将向量的相应分量相乘,然后对这些乘积求和来计算的。
点积的一个关键特征是,当向量指向相似或相反方向时点积较大(正或负),而当向量垂直时点积较小(或为零)。这使得点积在各种应用中非常有用,例如确定两个向量是否正交、计算空间中向量之间的角度,或者在更复杂的物理和工程操作(例如计算功或扭矩)中。在机器学习和数据科学中,点积在神经网络等算法中发挥着重要作用,有助于计算输入的加权和。
教程
我们将使用 SingleStore Notebooks 来执行本教程。如果您还没有,请免费激活 SingleStore 试用版以开始使用。让我们通过实践教程更深入地了解前面提到的方法。
让我们以两只宠物(猫和狗)为例,并在 3D 空间中将它们可视化。我们将尝试找出这两个宠物之间的曼哈顿距离、欧几里德距离、余弦距离和点积。

注册后,单击“笔记本”选项卡并创建一个带有名称的空白笔记本。
您可以开始在新创建的笔记本中运行代码。首先,安装并导入所需的库。
!pip 安装 numpy
!pip 安装 matplotlib
将 matplotlib.pyplot 导入为 plt
将 numpy 导入为 np定义可以用三个维度表示的宠物属性。由于宠物是具有许多特征的复杂实体,因此您需要将其简化为 3D 表示。这是一个例子:
从 mpl_toolkits.mplot3d 导入 Axes3D
# 宠物属性示例:[体重、身高、年龄]
# 这些是用于说明目的的假设数字
狗 = [5, 30, 2]
猫 = [3, 25, 4]
图 = plt.figure()
ax = Fig.add_subplot(111, 投影='3d')
# 绘制宠物图
ax.scatter(狗[0], 狗[1], 狗[2], label="狗", c='蓝色')
ax.scatter(cat[0], cat[1], cat[2], label="猫", c='绿色')
# 从原点到点绘制直线
ax.quiver(0, 0, 0, 狗[0], 狗[1], 狗[2], 颜色='蓝色',
箭头长度比率=0.1)
ax.quiver(0, 0, 0, cat[0], cat[1], cat[2], color='绿色',
箭头长度比率=0.1)
# 标记轴
ax.set_xlabel('体重(公斤)')
ax.set_ylabel('身高(厘米)')
ax.set_zlabel('年龄(岁)')
# 设置限制以实现更好的可视化
ax.set_xlim(0, 10)
ax.set_ylim(0, 40)
ax.set_zlim(0, 5)
# 添加图例和标题
斧头图例()
ax.set_title('宠物的 3D 表示')
plt.show()执行代码后,您应该能够看到此 3D 空间中提到的宠物的表示。
L1 = [abs(dog[i] - cat[i]) for i in range(len(dog))]
曼哈顿距离 = sum(L1)
print("曼哈顿距离:", manhattan_distance)