
很多时候,当我查看一些与 AI 相关的主题、教程或文章时,我发现图形搜索问题作为 AI 代理工作方式的示例呈现。那么,为什么会这样呢?一些经典的图形搜索问题与AI之间有什么关系?
您可能还喜欢:
Neo4j 中的图形算法:所有对最短路径
什么是人工智能?
环顾四周,你会发现人工智能没有明确而单一的定义。有人说,”人工智能被定义为对理性代理人的研究”,其中”理性的代理人可以是任何做出决策的东西,比如人、公司、机器或软件。它在考虑过去和当前感知(代理在给定实例上的感知输入)后,执行具有最佳结果的行动”。其他的定义则更具有哲学意义,试图找到人类自然智能和机器能做什么之间的界限。
但是,所有的定义都试图说,当你想知道该做什么时,AI 实际上是一门学科。这里来了一个理性的代理,通过一些传感器感知环境,并查看它已经执行的旧操作,它试图选择下一个可能获得最佳结果的操作。
因此,让我们来看看一个典型的路由查找问题。我们有一个具有许多节点的图形,您尝试在两个节点之间找到成本最低的路径。这里来了AI代理的定义。你并不完全知道路径是什么,一个理性的代理,通过感知环境,在我们的图中,将找到该路径。
但我们知道,有许多算法能够解决图形搜索问题。只需看看 DFS、BFS、Dijkstra 或A+。我们有些人从高中就知道这个算法。有什么新鲜点吗?这实际上就是AI代理所做的吗?嗯,是的,但不只是这个。AI不仅仅是一个编程范式,就像图形搜索算法一样,而且,正如我之前所说,它是对研究环境并尝试选择最佳结果的理性代理的研究。
AI 代理是一个广义的术语。它们包括机器学习、神经网络、深度学习等,并用于金融、医疗机构、安全等领域。因此,图形搜索只是 AI 的一个小子类型。
经典图形搜索算法和能够找到两个节点之间最短路径的 AI 代理之间的区别只是术语的差异
旧学校算法
实现图形搜索的方法有很多种。有经典的算法,如BFS和DFS,能够找到目标节点,而无需计算最佳路径,有算法,如Unifrom成本搜索,Dijkstra,或A+能够计算从源到目标的最短路径。所有这些算法都是基于树的算法,其中唯一的捕获点是图形与树不同,可能包含周期。
所有这些算法的要点是,在我们访问一个节点后,我们必须选择下一个未访问的节点并”访问”它,以查看我们是否达到了目标。
关于 BFS 更多
就像我之前说过的,广度优先搜索是一种基于树的算法。它的名称来自图形遍历是按层显示的想法。从源节点开始,我们首先探索邻居,然后进一步向下移动。
让我们来看看下面的图片:
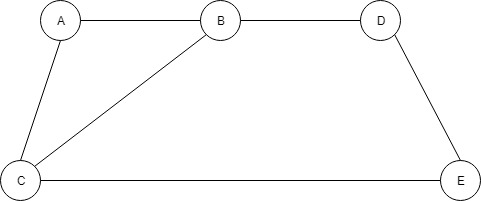
从节点 A 开始,我们看到此图形如何转换为树。
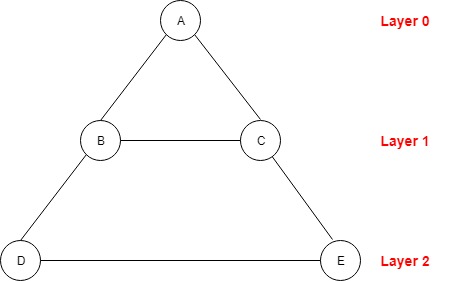
A 是留在第 0 层上的起始节点,然后 B 和 C 位于第 1 层,然后 D 和 E 位于第 2 层。这是 BFS 遍历此图形的顺序。
如果我们使用 BFS 遍历此图形,订单将为:A -> B -> C -> D -> E。
仔细观察树,就会发现B和C、E和D之间有一些联系。这是因为我们的图形包含周期。但是,如果我们想要以最佳方式遍历它,我们不应再次访问已访问的节点。因此,选择要访问的节点时,其中一个条件是不可访问。
算法的工作原理
考虑到,在我们访问开始节点后,我们将继续访问其所有邻居,然后我们将转到下一个”层”,并且需要一个队列。当我们访问一个节点时,我们会检查其邻居,如果邻居尚未访问,我们会将它们添加到队列中。然后,我们实际上只是从队列中选择下一个要访问的节点。我们需要做的另一件事是标记已访问的节点不再访问它们。这样,我们将只访问所有图形节点一次。
让我们来看看伪代码:
BFS(G, s, goal)
Let Q be queue
Q.enqueue(s)
Mark s as visited
while (Q is not empty)
//Removing that vertex from queue
v = Q队列(w)
标记 w 作为已访问
因此,使用此算法,如果开始节点和目标之间至少有一条路径,我们可以找到任何节点。
查找成本最低的路径
让我们通过在顶点上添加一些成本来更改图形。
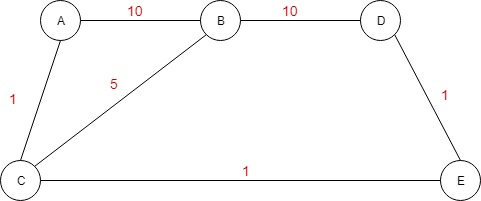
现在,我们希望以最低的成本从 A 转到 D。我们看到,从A到D有多种方法。我们可以走这条路,A & gt; B -> D,成本为 20,也可以选择 A -> C -> B -> D,成本较低,为 16。但还有另一条成本最低的路径,A -> C -> E -> D。那么,我们应该怎么做才能找到这条道路呢?我们需要改变访问下一个节点的方式。在经典的 BFS 算法中,我们使用 FIFO 队列顺序(先到先出)选择要访问的下一个节点。我们最终会找到目标,但不是最便宜的途径。为了以最低的成本到达路径上的目标,我们需要更改从队列访问下一个节点的方式。
我要向你们介绍的算法叫做统一成本搜索,这是Dijkstra的一个稍加修改的版本,当我们找到目的地时,我们会停止。经典的 Dijkstra 算法继续访问所有节点,直到队列为空,找到从开始节点到图形中所有其他节点的最小成本。与 BFS 不同的是,在这里,我们必须存储一个新值,该值表示从开始到当前访问的节点的总成本。
队列不会由 FIFO 规则排序,相反,我们将根据当前成本到目前为止的值对队列进行排序,并优先选择到目前为止成本最低的未访问的节点。
让我们来看看代码:
UniformCostSrearch(G, s)
s.costSoFar = 0;
for all nodes w in G except s
w.costSoFar = Int.maxInt
Let Q be a priority queue ordered by cost_so_far
Q.enqueue(s)
while (Q is not empty)
//Removing that vertex from queue
v = Q.dequeue()
If v is goal
return “found the goal”
//processing all the neighbours of v
for all neighbours w of v in Graph G
currentCost = dist[v,w]
newCost = v.costSoFar + currentCost;
If (newCost < w.costSoFar)
w.costSoFar = newCost ;
Q.enqueue(w)
这样,我们将根据每个节点到目前为止的最低成本选择下一个要访问的节点。
但到目前为止,最低成本需要更新,因为通过浏览图形,我们始终可以找到更好的方法来到达节点成本至今 = 当前成本;
如果(新成本 < w.成本已过) |
w.成本AuFar = 新成本;
Q.队列(w);
}
如果新成本较低,这意味着我们找到了更好的方法来到达该节点,并且到目前为止我们更新了该成本。在这里,您可以看到有关此算法的更多详细信息,以及如何使用一些估计值来改进它,从而将其转换为 A+。
图形搜索与人工智能有何关系?
好吧,让我们回顾一下什么是AI。正如我之前说过的,人工智能被定义为对理性代理人的研究,理性代理可以是任何做出决策(如人、公司、机器或软件)的人。在考虑过去和当前感知(代理在给定实例上的感知输入)后,它会执行具有最佳结果的操作。
图形搜索算法能得到什么?我们得到一个函数、一个程序、一个代理,它给定一个图形、一个环境和一个开始节点,通过考虑过去和当前的感知,计算一系列用于查找目标节点的操作。
嗯,我们在这里可以看到,图形搜索算法的作用符合AI代理的定义。因此,我们有一个基本形式的AI。你看这里,AI不完全是火箭科学。定义足够宽,可以包括简单的算法作为图形搜索。这些示例为我们提供了了解 AI 基本概念的方法。
考虑到 AI 概念,让我们编写一个 AI 代理来分析环境并计算一系列有助于我们实现目标的操作(我们基本上将构建图形搜索算法,但使用 AI 术语)。
下面是罗马尼亚的地图。
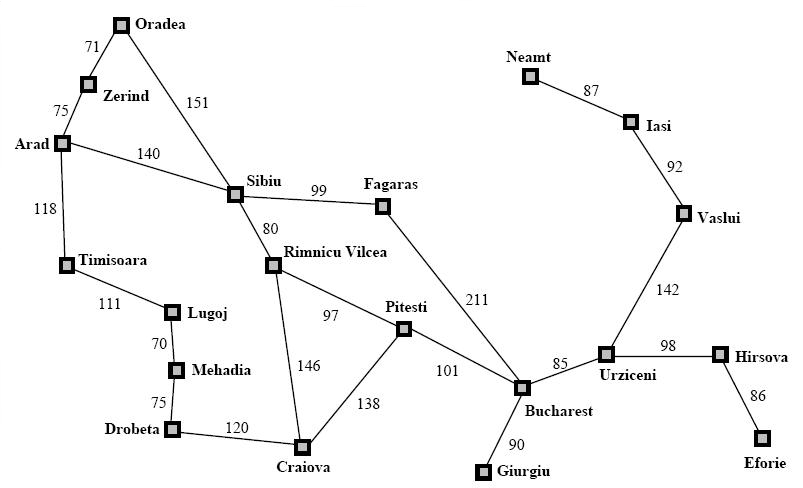
比想的是,我们在阿拉德,我们想去,在最短的道路上,布加勒斯特。我们可以看到,我们可以采取多条路线。我们可以从阿拉德到蒂米索拉,然后卢戈伊,等等,或者我们可以选择西比乌,然后法加拉,直接去布加勒斯特。但是我们不知道哪条路的成本最低。
问题的定义是什么?
问题可以在多个组件中分解:
- 我们有一个初始状态:在阿拉德
- 我们有一个函数操作。当我们处于状态时,它返回一组可能的操作。例如:在阿拉德,我们可以去泽林德、西比乌或提米索拉
- 我们有一个函数结果 (s, a) -> s ‘ 。处于状态,如果我们应用行动a,我们将去s’
- 我们有一个目标测试函数目标测试 (s) -> t/f。它告诉我们,如果我们达到了目标
- 步骤成本 (s,a,s’) -> 行动成本。它告诉我们从 s 到 s 使用操作的步长成本
- 成本(S1 -> S2 -> … – > Sn) -> n(路径成本)。总路径成本
现在,让我们来看看如何映射我们的目标查找问题所有可能的状态都称为状态空间。我们必须通过应用操作和从状态到状态来探索状态空间。从 Arad 开始并应用函数操作(”Arad”),我们将得到三个可能的操作。去泽林,提米索拉,或西比乌。现在,考虑到这一点,我们可以将状态空间分为三个部分:
- 我们有探索的国家部分(例如,现在只有阿拉德)
- 我们有边界我们称之为最远的州(蒂米索拉,泽林德和西比乌)
- 和未探索的状态:所有其他城市
因此,作为探索状态的一部分,我们需要从边界选择一个新的状态,应用一个行动,并移动到该状态,从而扩展边界。
TreeSearch(G, s)
s.costSoFar = 0;
for all nodes w in G except s
w.costSoFar = Int.maxInt
Let frontier be a priority queue ordered by the cost_so_far
frontier.enqueue(s)
while (frontier is not empty)
//Removing that vertex from frontier,whose neighbour will be visited now
v = frontier.dequeue()
If v is goal
return “found the goal”
//processing all the neighbours of v
for all neighbours w of v in Graph G
currentCost = dist[v,w]
newCost = v.costSoFar + currentCost;
If (newCost < w.costSoFar) {
w.costSoFar = newCost ;
frontier.enqueue(w)
因此,我们有一个边界,首先,它只包含到开始节点中。然后,在每次迭代中,我们从边界获取元素,我们移动到下一个状态,如果我们达到目标,我们将退出消息”找到目标”。或者,我们还可以打印路径。否则,我们将新状态添加到边界。
现在,根据如何从边界获取新状态,您可以实现经典 BFS、统一成本搜索或 A+ 算法。在这里,你可以更清楚地看到这些算法和检测从阿拉德到布加勒斯特的最短路径的最佳算法之间的差异。
结论
当然,AI 代理不会恢复为只是图形搜索。我们有用于人脸识别的 AI 算法,我们有机器学习、神经网络和基于统计的算法,其中唯一的限制是数学。但是,这不必吓唬,因为基本概念并不难理解。
进一步阅读
