Posted by on | Featured

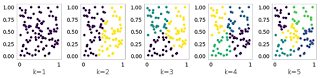
我们以前已经看到了如何实现 k 手段。但是, 该算法的结果在很大程度上取决于参数 k 的选择。在这篇文章中, 我们将看到如何使用差距统计以最佳方式选择 k。该方法的主要思想是比较数据到聚类的聚类惯性和参考数据集。k 的最优选择是由 k 给出的, 两者的间隙最大。为了说明这个想法, 让我们选择一个均匀分布的点集作为参考数据集, 并查看 k 均值增加 k 的结果:

import numpy as np
import matplotlib.pyplot as plt

from sklearn.datasets import make_blobs
from sklearn.metrics import pairwise_distances
from sklearn.cluster import KMeans


reference = np.random.rand(100, 2)
plt.figure(figsize=(12, 3))
for k in range(1,6):
    kmeans = KMeans(n_clusters=k)
    a = kmeans.fit_predict(reference)
    plt.subplot(1,5,k)
    plt.scatter(reference[:, 0], reference[:, 1], c=a)
    plt.xlabel('k='+str(k))
plt.tight_layout()
plt.show()

现在, 让我们对具有三个自然群集的目标数据集执行相同的操作:

plt.figure(figsize=(12, 3))
for k in range(1,6):
    kmeans = KMeans(n_clusters=k)
    a = kmeans.fit_predict(X)
    plt.subplot(1,5,k)
    plt.scatter(X[:, 0], X[:, 1], c=a)
    plt.xlabel('k='+str(k))
plt.tight_layout()
plt.show()

如果我们绘制这两种情况下的惯性, 我们注意到, 在参考数据集上, 惯性下降非常缓慢, 而在目标数据集上, 它假定一个弯头的形状:

def compute_inertia(a, X):
    W = [np.mean(pairwise_distances(X[a == c, :])) for c in np.unique(a)]
    return np.mean(W)

def compute_gap(clustering, k_max=10, n_references=5):
    reference_inertia = []
    for k in range(1, k_max+1):
        local_inertia = []
        for _ in range(n_references):
            clustering.n_clusters = k
            assignments = clustering.fit_predict(reference)
            local_inertia.append(compute_inertia(assignments, reference))
        reference_inertia.append(np.mean(local_inertia))

    ondata_inertia = []
    for k in range(1, k_max+1):
        clustering.n_clusters = k
        assignments = clustering.fit_predict(X)
        ondata_inertia.append(compute_inertia(assignments, X))

    gap = np.log(reference_inertia)-np.log(ondata_inertia)
    return gap, np.log(reference_inertia), np.log(ondata_inertia)

gap, reference_inertia, ondata_inertia = compute_gap(KMeans())


plt.plot(range(1, k_max+1), reference_inertia,
         '-o', label='reference')
plt.plot(range(1, k_max+1), ondata_inertia,
         '-o', label='data')
plt.xlabel('k')
plt.ylabel('log(inertia)')
plt.show()

现在, 我们可以计算每个 k 的差距统计值, 计算上面显示的两条曲线的差异:

plt.plot(range(1, k_max+1), gap, '-o')
plt.ylabel('gap')
plt.xlabel('k')

很容易看出, 对于 kc我方3来说, 差距是最大的, 这正是我们目标数据集的正确选择。

Tags: ,
Comments are closed.