数学不是关于数字、方程、计算或算法的:它是关于理解的。
• 威廉·保罗·瑟斯顿
有几个工具和技术不需要任何数学专业知识来解决数据科学问题。但是,本文旨在探讨一旦有效地完成特征工程和数据预处理,一些数学分支如何帮助磨练数据科学方面的科学和工程专业知识。
在前进之前,我们需要确保数据分析做得正确,因为它是通过数据科学解决业务问题的基础。
快速回顾不同级别的分析:

并非所有业务问题都必须经过各个级别的分析。有时,简单的描述性分析可以帮助利益相关者进行决策。
让我们探讨一些数学课程如何帮助我们更好地理解数据科学领域。
描述性分析
数据预处理后,研究和解释数据非常重要。在收集和分析数值数据时,统计数据会派上用场。虽然数学和统计学听起来两个像不同的领域,他们不是;统计学是数学的一个分支,它处理数据的收集、组织、分析、解释和呈现。
表示利用描述性统计信息的数据的一些示例包括:
- 在季风期间,海得拉巴的天气平均在30摄氏度左右。有时,它低至19摄氏度。
- 数学课的考试成绩从60%到90%不等,分数频率较高,在70%左右。
- 在财政年度提交的所得税退税数量(在年末达到峰值,因此数据集很可能出现负/左偏斜)。
描述性统计提供了强大的计算,如平均值、中位数、模式、偏差、方差、范围,我们可以通过这些计算得出有意义的数据摘要。
诊断分析
虽然了解问题的根本原因可能有助于更有效地预测业务结果,但找到这些原因并不总是那么容易。特征工程有助于缩小潜在原因。
相关性分析有助于识别变量之间的关系。下面的漫画描述了相关性和因果关系是如何不同的(来源:https://xkcd.com/925/)。
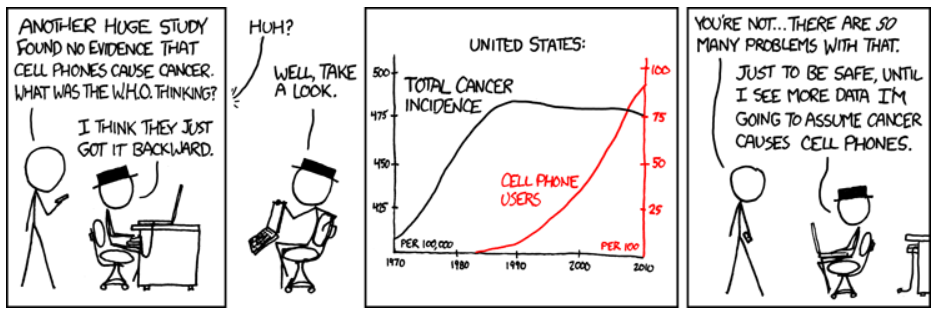
虽然相关性不一定证明因果关系的合理性,但它确实有助于确定关系,并有助于优化,从而进行规范性分析。
相关性分析假定变量之间的相关性是线性的。线性代数有助于建立变量之间关系的线性和强度。事实上,线性代数不仅在诊断分析中起着至关重要的作用,而且在文本分析和人工智能中起着至关重要的作用。线性代数在多维空间中运行;因此,一旦转换为数学方程,就很容易解决任何类型的业务问题
使用假设场景预测具有一定可靠性的未来…听起来像我们在学校学习的数学方程,对吗?
线性代数有助于用方程来表示问题。变量和方程可以以矢量的形式表示。无论变量和方程的数量,我们都能找到满足约束的解决方案。
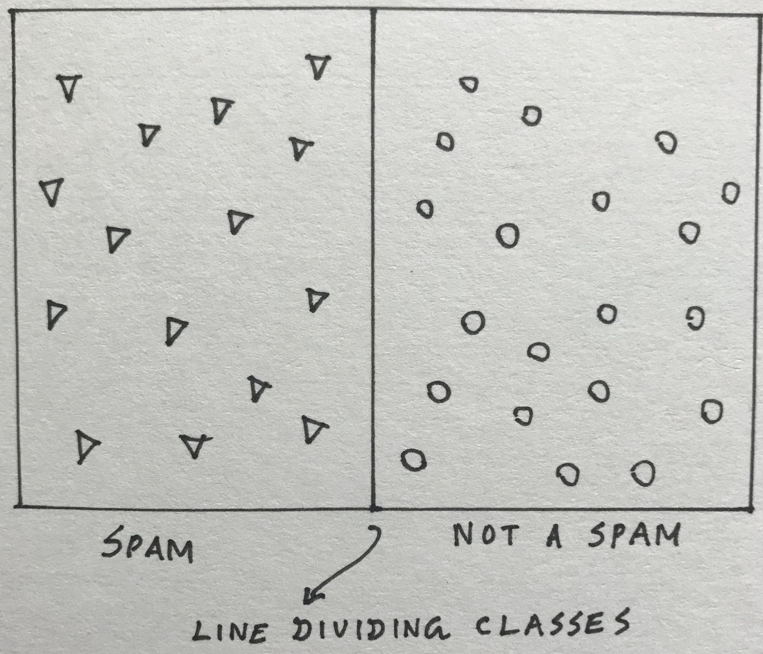
在分类问题(如预测新电子邮件是否为垃圾邮件)中,绘制此行将划分垃圾邮件和非垃圾邮件的空间并相应地放置新数据。
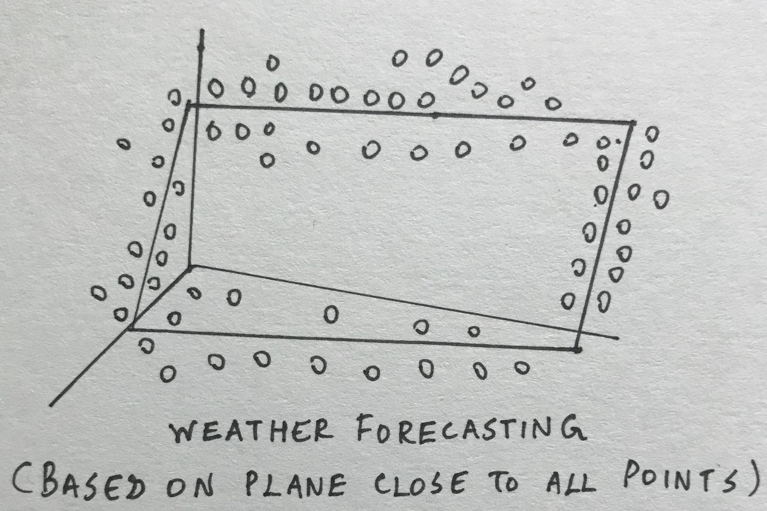
在预测用例(如天气预报)中,它是所有关于确定最接近所有历史数据点的平面(来自以前几天/月/年的天气)。
规定性分析
几乎所有业务问题都有限制(时间、预算、资源等)。根据这些约束提供我们的建议,具有很高的可靠性至关重要。
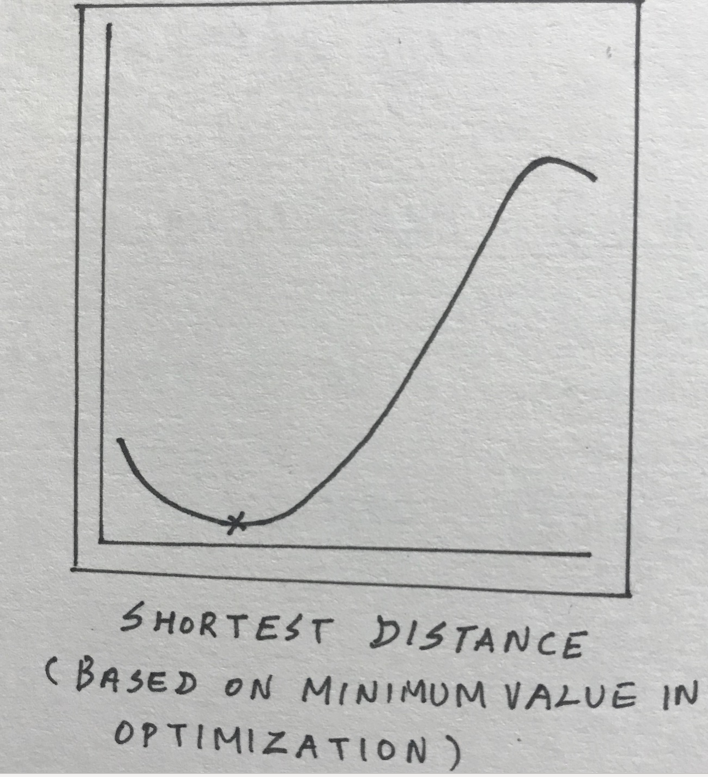
线性编程和线性优化有助于通过线性函数表示变量之间的复杂关系,并找到最佳点。
 Z
Z
数学优化中的最大值、最小值、梯度下降和其他类似概念,在解决复杂问题时得到拯救。
由于处方是基于未来事件,因此提供建议及其可量化的可能性非常重要。因此,概率理论与优化技术一起起起起起起着至关重要的作用。
总结
数学的以下分支通过分析数据模式并具有较高的可靠性来解决这些问题,从而有助于理解业务问题。
-
描述性统计:了解数据模式。
-
线性代数:将业务问题转化为数学问题并加以解决。事实上,线性代数具有以矢量和指标的形式表示数字和文本数据的强大功能,在人工智能的深入学习领域也发挥着强大的作用。
-
线性编程:提供具有给定约束的最佳结果。
-
概率:提供可量化的可能性以及建议。
当然,其他分支,如微积分,在深度学习中起着至关重要的作用。
在我看来,通过数据科学在解决业务问题方面增加数学风格提供了更多选项,提高了可靠性。
我在下面列出了一些我最喜欢的链接,以更有趣的方式探索数学。愉快的探索!
com/
