数据科学数学和统计学的完整指南

正如乔希·威尔斯曾经说过的

“数据科学家比任何程序员都更善于统计，也比任何统计人员都更善于编程。

数据科学的数学和统计是必不可少的，因为这些门徒构成了所有机器学习算法的基本基础。事实上，数学是我们周围一切事物的背后，从形状、图案和颜色，到花瓣的计数。数学植根于我们生活的方方面面。

虽然对编程语言有很好的理解，但机器学习算法和采用数据驱动方法对于成为数据科学家是必要的，但数据科学并不全是这些领域的。在本博客文章中，您将了解数学和统计对数据科学的重要性，以及如何使用它们来构建机器学习模型。

以下是我将在本数学和数据科学统计博客中介绍的主题列表：

1. 统计简介
2. 统计术语
3. 统计中的类别
4. 了解描述性分析
5. R 中的描述性统计信息
6. 理解推断分析
7. R 中的推断统计

您可能还喜欢：大数据：数据科学和高级分析。

统计简介

要成为一个成功的数据科学家，你必须知道你的基本知识。数学和统计是机器学习算法的构建基块。了解各种机器学习算法背后的技术非常重要，以便了解如何以及何时使用它们。现在问题出现了，统计究竟是什么？

统计学是一门与数据收集、分析、解释和演示有关的数学科学。

统计与数据科学的数学和统计

统计用于处理现实世界中的复杂问题，以便数据科学家和分析人员可以查找数据中有意义的趋势和变化。简单来说，统计可以通过对数据执行数学计算来从数据中获得有意义的见解。

实现多个统计函数、原则和算法，以分析原始数据、构建统计模型并推断或预测结果。

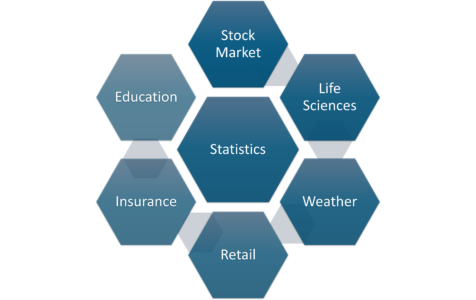
统计应用 – 数据科学的数学和统计

统计领域对生活的所有领域都有影响，股票市场、生命科学、天气、零售、保险和教育仅举几例让我们讨论统计中的基本术语。

统计术语 – 数据科学统计

在处理数据科学统计时，应了解几个关键统计术语。我在下面讨论了这些术语：

• 总体是必须从中收集数据的一组源。
• 样本是总体的子集
• 变量是可测量或计数的任何特征、数量或数量。变量也可以称为数据项。
• 统计参数或总体参数也称为统计模型，是索引概率分布系列的数量。例如，总体的平均值、中位数等。

在我们进一步讨论统计信息类别之前，让我们看一下分析的类型。

分析类型

任何事件的分析可以通过两种方式之一完成：

例如，如果我想从星巴克购买咖啡，它有短，高和格兰德。这是定性分析的一个例子。但是，如果一家商店每周销售70种普通咖啡，这是定量分析，因为我们有一个数字代表每周销售的咖啡。

虽然这两种分析的目的是提供结果，但定量分析提供了更清晰的图像，因此在分析中至关重要。

统计中的类别

统计中有两个主要类别，即：

1. 描述性统计
2. 推断统计

描述性统计

描述性统计使用数据通过数值计算或图形或表提供总体描述。

描述性统计有助于组织数据，并侧重于提供参数的数据的特征。

描述性统计示例 – 数据科学的数学和统计

推断统计

推断统计基于从相关总体获取的数据样本对总体进行推断和预测。

推断统计概括了大型数据集，并应用概率得出结论。它允许您基于样本统计信息推断总体参数，并在此基础上构建模型。

推断统计与数据科学的数学和统计

因此，如果我们考虑在”推断统计”中查找班级中学生平均身高的同一示例，您将对该类进行一组示例，该示例集基本上是整个班级中的几个人。你已经把班级分为高、平均和矮。在此方法中，您基本上构建一个统计模型，并将其扩展到类中的全部总体。

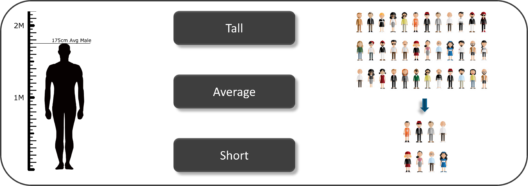推断统计示例 – 数据科学的数学和统计

现在，让我们将注意力集中在描述性统计上，看看它如何用于解决分析问题。

了解描述性分析

当我们尝试以图形的形式表示数据时，如直方图、线图等，数据是基于某种中心趋势表示的。中央趋势度量，如，平均值，中值，或点差的度量，等用于统计分析。为了更好地理解统计，让我们通过一个示例来讨论统计中的不同度量。

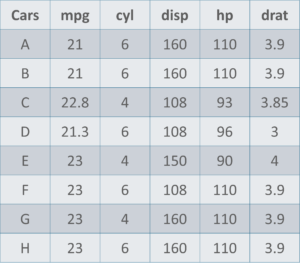汽车数据集 – 数据科学的数学和统计

下面是包含变量的汽车示例数据集：

1. 汽车
2. 每加仑里程（英里）
3. 气缸类型（缸）
4. 位移（分量）
5. 马力 （hp）
6. 实际轴比（德拉特）。

在进一步行动起来之前，先确定中央主要措施或中心趋势措施。

中心措施

1. 平均值：样本中所有值的平均值度量称为平均值。
2. 中位数：样本集的中心值度量称为”中位数”。
3. 模式：示例集中最重复的值称为”模式”。

使用描述性分析，您可以分析样本数据集中的每个变量，包括平均值、标准偏差、最小值和最大值。

• 如果我们想要找出汽车在汽车人口中的平均或平均马力，我们将检查和计算所有值的平均值。在这种情况下，我们将采用每辆车的马力之和，除以汽车总数：

均值 = （110*110*93*96*90*110*110*110*110）/8 = 103.625

• 如果我们想要找出 mpg 在汽车数量中的中心值，我们将按升序或降序排列 mpg 值，并选择中间值。在这种情况下，我们有 8 个值，这是一个偶数条目。因此，我们必须采用两个中间值的平均值。

8辆车的mpg： 21，21，218,23,23,23,23
中位数 = （22.8+23 ）/2 = 22.9

• 如果我们想要找出汽车人口中最常见的气缸类型，我们将检查重复次数最多的值。在这里我们可以看到，气缸有两个值，4 和 6。查看数据集，可以看到最重复值为 6。因此，6是我们的模式。

价差措施

与中心度量一样，我们也有点差的度量，其中包括以下措施：

1. 范围：它是数据集中值分布方式的给定度量值。
2. 四分位数范围 （IQR）：它是基于将数据集划分为四分位数的可变性的度量。
3. 差异：它描述了随机变量与其预期值的不同程度。它需要计算偏差的平方。
   1. 偏差是每个元素与均值之间的差值。
   2. 总体方差是平方差的平均值
   3. 样本方差是与平均值的平方差的平均值
4. 标准偏差：它是一组数据从平均值的分散量的度量。

现在，我们已经看到了描述性分析背后的统计数据和数学，让我们尝试在 R 中解决它。

R 中的统计信息

世界向R移动的原因有很多。其中一对夫妇在下面登记：

• R 是开源的，可免费使用。与 SAS 或 Matlab 不同，您可以自由安装、使用、更新、克隆、修改、重新分发和转售 R。
• R 是跨平台兼容的。它在 Windows、Mac OS X 和 Linux 上运行是兼容的。它还可以从微软Excel、微软访问、MySQL、SQLite、甲骨文和其他程序导入数据。
• R 是一种功能强大的脚本语言，它可以处理大型、复杂的数据集。
• R高度灵活且不断发展。统计领域的许多新发展首先显示为 R 包。

现在，让我们继续前进，在 R 中实现描述性统计信息。

R 中的描述性统计信息

最好执行实际实现以更好地了解概念。在本节中，我们将执行一个小演示，向您展示如何计算平均值、中位数、模式、方差、标准偏差以及如何通过绘制直方图来研究变量。这是一个相当简单的演示，但它也构成了每个机器学习算法的基础。

步骤 1：导入数据进行计算

>set.seed(1)
#Generate random numbers and store it in a variable called data
>data = runif(20,1,10)

第 2 步：计算数据的平均值

#Calculate Mean
>mean = mean(data)
>print(mean)

[1] 5.996504

第 3 步：计算数据的中位数

#Calculate Median
>median = median(data)
>print(median)

[1] 6

最大值（表格（匹配（x，ux）））
}
>结果 <- 模式（数据）>打印（数据）

[1] 3.389578 4.349115 6.155680 9.173870 2.815137 9.085507 9.502077 6.947180 6.662026
[10] 1.556076 2.853771 2.589011 7.183206 4.456933 7.928573 5.479293 7.458567 9.927155
[19] 4.420317 7.997007

>cat（”模式==”，结果）

模式 = 3.389578

第 5 步：计算数据的方差和 Std 偏差

#Calculate Variance and std Deviation
>variance = var(data)
>standardDeviation = sqrt(var(data))
>print(standardDeviation)

[1] 2.575061

第 6 步：绘制直方图

#Plot Histogram
>hist(data, bins=10, range= c(0,10), edgecolor='black')

直方图用于显示数据点的频率：

到目前为止，您已经了解了描述性统计，现在让我们来谈谈推断统计5雷姆;字体系列：”=理解推断分析

统计学家使用假设检验来正式检查该假设是被接受还是被拒绝。假设检验是一种推断统计技术，用于确定数据样本中是否有足够的证据来推断特定条件对整个总体适用。

在一般总体特征下，我们随机抽取样本并分析样本的特性。我们测试确定的结论是否准确代表总体，最后我们解释他们的结果。是否接受该假设取决于我们从该假设中获得百分比值。

为了更好地理解这一点，我们来看一个示例。

想想四个男孩，尼克，约翰，鲍勃和哈利，他们被发现在上课时偷课。他们被要求留在学校，打扫教室作为惩罚。

推断分析 » 数据科学的数学和统计 » Edureka

于是，约翰决定他们四个人轮流打扫教室。他想出了一个计划，写他们的名字，在chits上，并把它们放在一个碗

现在已经三天了，除了约翰的名字，每个人都来了！假设这个事件是完全随机的，没有偏见，约翰不作弊的概率是多少？

让我们首先计算约翰一天不被选中的概率：

P（约翰一天不挑） = 3/4 = 75%

这里的概率是 75%，这是相当高的。现在，如果约翰连续三天没有被选中，概率下降到42%

P（约翰 3 天未采摘） = 3/4 ±3/4 × 3/4 = 0.42 （约）

现在，让我们考虑一个情况，约翰连续 12 天没有被选中！概率下降到3.2%。因此，约翰作弊的可能性相当高。

P（约翰 12 天未采摘） = （3/4） ±12 = 0.032 <?.??

为了使统计学家得出结论，他们定义了所谓的阈值。考虑到上述情况，如果阈值设置为 5%，则表明，如果概率低于 5%，则 John 正在欺骗他走出拘留。但是，如果概率高于阈值，那么 John 就是幸运的，他的名字不会被选中。

概率和假设检验产生两个重要概念，即：

• 空假设：结果与假设没有什么不同。
• 备选假设：结果推翻了这一假设。

因此，在我们的示例中，如果事件发生的概率小于 5%，则它是一个偏置事件，因此它批准备用假设。

R 中的推断统计

在本演示中，我们将使用间隙设置器数据集来执行假设检验。gapminder数据集包含142个国家的清单，其中分别列有1952年至2007年每五年的预期寿命、人均国内生产总值和人口值。

我们将首先下载隔空程序包并将其加载到我们的 R 环境中：

#Install and Load gapminder package
install.packages("gapminder")
library(gapminder)
data("gapminder")

现在，让我们使用 R 中的 View（） 函数来了解一下我们的数据集：

#Display gapminder dataset
View(gapminder)

以下是我们的数据集：

下一步是加载由 R 提供的臭名昭著的 dplyr 包。我们特别希望使用管道 （%>%）dplyr 包中的运算符。对于那些不知道管道操作员操作人员操作的人员，它基本上允许您将数据从左侧输送到管道右侧的数据中。这是相当不言自明的。

#Install and Load dplyr package
install.packages("dplyr")
library(dplyr)

我们的下一步是比较两个地方（爱尔兰和南非）的预期寿命，并执行 t 检验以检查比较是否遵循空假设或替代假设。

#Comparing the variance in life expectancy in South Africa & Ireland
df1 <-gapminder %>%
select(country, lifeExp) %>%
filter(country == "South Africa" | country =="Ireland")

因此，在将 t 检验应用于数据框 （df1） 并比较预期寿命后，您可以看到以下结果：

#Perform t-test

t.test(data = df1, lifeExp ~ country)

Welch Two Sample t-test

data: lifeExp by country
t = 10.067, df = 19.109, p-value = 4.466e-09
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
15.07022 22.97794
sample estimates:
mean in group Ireland mean in group South Africa
73.01725              53.99317

请注意，在爱尔兰组和南非，您可以看到预期寿命几乎相差 20。现在，我们需要检查南非和爱尔兰的预期寿命价值差异是否真正有效，而不仅仅是单纯的偶然性。因此，进行了 t 检验。

特别注意 p 值也称为概率值。p 值是一个非常重要的度量，当涉及到确保模型的重要性时。仅当 p 值小于预先确定的统计显著性级别（理想情况下为 0.05）时，模型才具有统计显著性。正如您从输出中看到的，p 值为 4

在模型的摘要中，请注意另一个重要参数，称为 t 值。较大的 t 值表明替代假设为真，并且平均寿命的差异不等于纯运气为零。因此，在我们的案例中，零假设被否决。

在演示结束时，我们将为每个大陆绘制一个图表，以便该图显示每个大陆的预期寿命如何随该大陆的人均 GDP 而变化。

#Plotting a gdpPercap vs lifeExp graph for each continent
#Install and Load ggplot2 package
install.packages("ggplot2")
library(ggplot2)
gapminder%>%
filter(gdpPercap < 50000) %>%
ggplot(aes(x=log(gdpPercap), y=lifeExp, col=continent, size=pop))+
geom_point(alpha=0.3)+
geom_smooth(method = lm)+
facet_wrap(~continent)

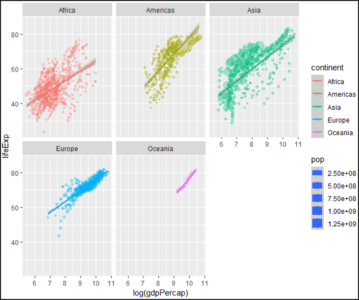
在上图中，您几乎可以看到每个大陆的预期寿命与人均 GDP 的线性差异。这还显示了 R 语言可用于统计分析的方面。

有了这个，我们来到这个博客的结尾。

进一步阅读

• 数据科学之旅。
• 顶级数据科学工具。
• 数据科学和机器学习的最佳Python库。