
R 中的随机林
随着对更复杂的计算的需求,我们不能依赖简单的算法。相反,我们必须利用具有较高计算能力的算法,其中一种算法是随机林。在关于随机林的博客文章中,您将通过使用R 语言了解随机林的基本原理及其实现。
您可能还喜欢:
使用决策树进行机器学习简介
什么是分类?
分类是预测给定输入数据点的类的方法。分类问题在机器学习中很常见,属于监督学习方法。
假设您希望将电子邮件分为两组:垃圾邮件和非垃圾邮件。对于此类问题,您必须将输入数据点分配给不同的类,则可以使用分类算法。
根据分类,我们有 2 种类型:
- 二进制分类
- 多类分类
分类 = R 中的随机林
我前面给出的将电子邮件分类为垃圾邮件和非垃圾邮件的示例是二进制类型的,因为在这里我们将电子邮件分为 2 类(垃圾邮件和非垃圾邮件)。
但是,假设我们想要将电子邮件分为 3 类:
- 垃圾邮件
- 非垃圾邮件
- 草稿
因此,在这里,我们将电子邮件分类为 2 个以上类,这正是多类分类的含义。
这里需要注意的一点是,分类模型通常预测连续值。但是,此连续值表示属于每个输出类的给定数据点的概率。
现在,您已经很好地了解了什么是分类,让我们来看看机器学习中使用的几个分类算法。
什么是随机林?
随机林算法是一种监督分类和回归算法。顾名思义,此算法随机创建具有多个树的林。
一般来说,森林中的树木越多,森林看起来就越坚固
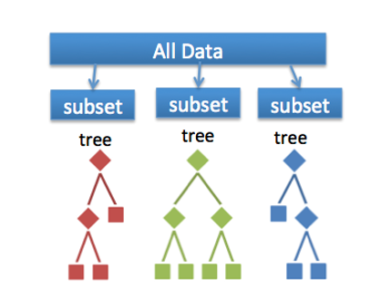
随机林
简而言之,随机林会生成多个决策树(称为林),并将它们粘在一起以获得更准确、更稳定的预测。它构建的森林是决策树的集合,使用装袋方法进行训练。
在深入讨论随机林之前,我们需要了解决策树的工作原理。
随机森林和决策树是相同的吗?
假设你想买房子,但你不能决定买哪一个。所以,你咨询了几个代理,他们给你一个参数列表,你应该考虑之前买房子。该列表包括:
- 房子的价格
- 地区
- 卧室数量
- 停车位
- 可用设施
这些参数称为预测变量,用于查找响应变量。下面是如何使用决策树表示上述问题陈述的图表图。
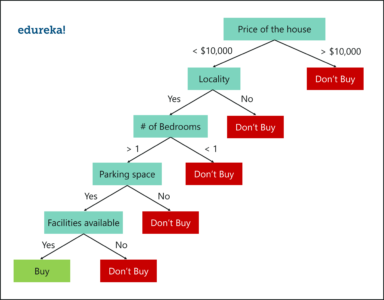 决策树示例
决策树示例
这里需要注意的一点是,决策树通过使用所有预测变量构建在整个数据集上。
现在,让我们看看随机林如何解决同样的问题。
正如我前面提到的,随机林是决策树的一个集合,它随机选择一组参数,并为每个选定的参数集创建决策树。
请看下图。
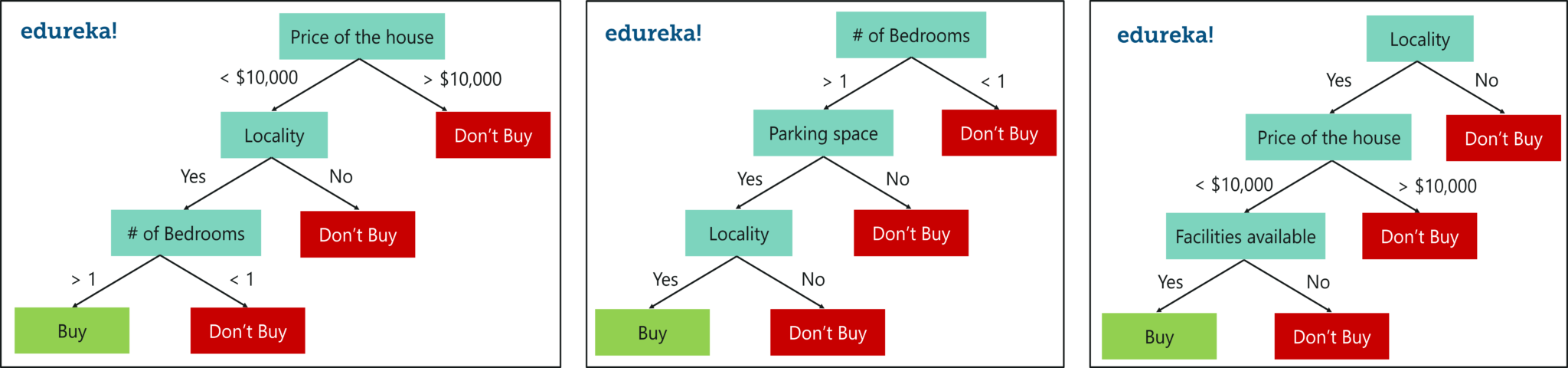
带 3 个决策树的随机林
在这里,我创建了 3 个决策树,每个树只从整个数据集获取 3 个参数。每个决策树基于该树中使用的相应预测变量预测结果,最后取取随机林中所有决策树的结果平均值
最后,决策树使用所有预测变量构建在整个数据集上,而随机林用于创建多个决策树,以便每个决策树仅生成在数据集的一部分上。
我希望决策树和随机森林的区别是明确的。
为什么要使用随机林?
尽管决策树方便且易于实现,但它们缺乏准确性。决策树使用用于构建它们的训练数据非常有效,但在对新样本进行分类时,它们并不灵活,这意味着测试阶段的准确性非常低。
由于过程称为”过度拟合”,因此会发生这种情况。
这意味着训练数据中的干扰被模型记录和学习为概念。但这里的问题是,这些概念不适用于测试数据,并且对模型对新数据进行分类的能力产生负面影响,从而降低了测试数据的准确性。
这是随机林的来临时。它基于装袋的概念,通过组合数据集不同样本上的多个决策树的结果来减少预测中的变异。
现在,让我们关注随机林。
随机林如何工作?
要了解随机林,请考虑以下示例数据集。其中,我们有四个预测变量:
- 重量
- 血流
- 阻塞动脉
- 胸痛
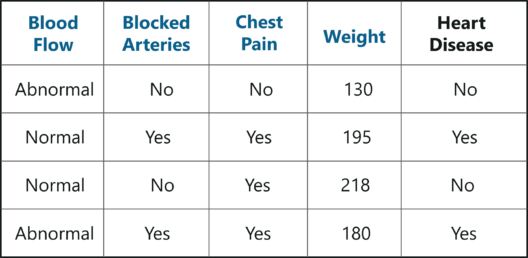
这些变量用于预测一个人是否患有心脏病。我们将使用此数据集创建一个随机林,用于预测一个人是否患有心脏病。
创建随机林
第 1 步:创建引导数据集
引导是一种估计方法,用于通过重新采样数据集对数据集进行预测这里需要注意的一点是,我们可以多次选择同一个示例。
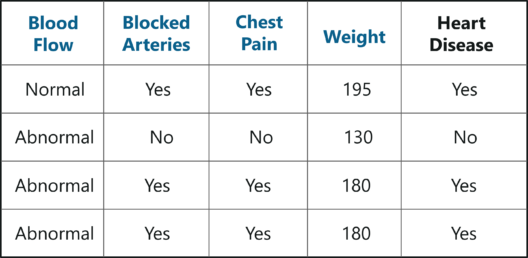
在上图中,我从原始数据集中随机选择样本,并创建了一个引导数据集。很简单,不是吗?那么,在现实世界的问题上,你永远不会得到这么小的数据集,因此创建一个引导式数据集要复杂一些。
第 2 步:创建决策树
- 我们的下一个任务是使用上一步创建的引导数据集来构建决策树。由于我们正在创建一个随机林,所以我们不会考虑我们创建的整个数据集。相反,我们在每个步骤中只使用变量的随机子集。
- 在此示例中,我们只考虑每个步骤中的两个变量。因此,我们从根节点开始,在这里我们随机选择两个变量作为根节点的候选变量。
- 假设我们选择了血流和阻塞的动脉。在这 2 个变量中,我们现在必须选择最能分离样本的变量。为了学习此示例,假设阻塞动脉是一个更重要的预测变量,因此将其指定为根节点。
- 我们的下一步是对每个即将推出的分支节点重复相同的过程。在这里,我们再次随机选择两个变量作为分支节点的候选变量,然后选择最能分离样本的变量。
像这样,我们构建树时只考虑每个步骤中的变量的随机子集。通过遵循上述过程,我们的树将如下所示:
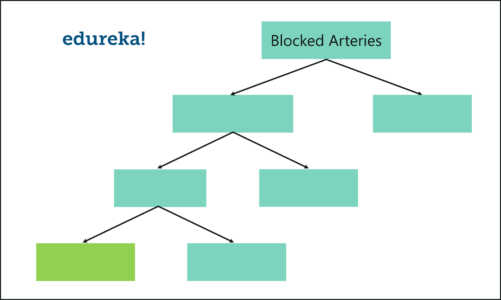 随机林算法 = R 中的随机林
随机林算法 = R 中的随机林
我们刚刚创建了第一个决策树。
步骤 3:返回步骤 1 并重复
正如我前面提到的,随机林是决策树的集合。每个决策树根据该树中使用的相应预测变量预测输出类。最后,记录随机林中所有决策树的结果,并将具有多数选票的类计算为输出类。
因此,我们现在必须通过在每个步骤中考虑随机预测变量的子集来创建更多的决策树。为此,请返回步骤 1,创建新的引导数据集,然后通过在每个步骤中仅考虑变量子集来生成决策树。因此,按照上述步骤操作,我们的随机林如下所示:
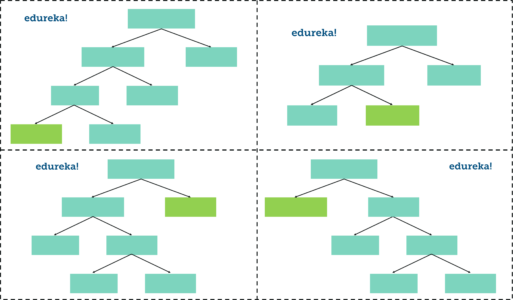 在随机林中拥有如此多样的决策树比使用所有要素和整个数据集创建的单个决策树更有效。
在随机林中拥有如此多样的决策树比使用所有要素和整个数据集创建的单个决策树更有效。
第 4 步:预测新数据点的结果
现在,我们已经创建了一个随机林,让我们来看看如何使用它来预测新患者是否患有心脏病。
下图显示了有关新患者的数据。我们要做的就是将这些数据运行到我们所做的决策树中。
第一棵树显示病人有心脏病,所以我们在表格中跟踪,如图所示。
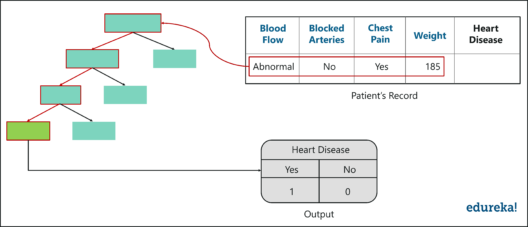
同样,我们沿着其他决策树运行此数据,并跟踪每个树预测的类。在随机林中运行所有树下的数据后,我们检查哪个类获得了多数票。在我们的例子中,”是”类获得最多票数,因此很明显,新病人有心脏病。
最后,我们引导数据并使用来自所有树的聚合来做出决定,此过程称为”Bagging”。
第 5 步:评估模型
我们的最后一步是评估随机林模型。早些时候,当我们创建引导数据集时,我们遗漏了一个条目/示例,因为我们复制了另一个示例。在实际问题中,原始数据集的大约 1/3 不包括在引导式数据集中。
下图显示了未在引导的数据集中结束的条目。
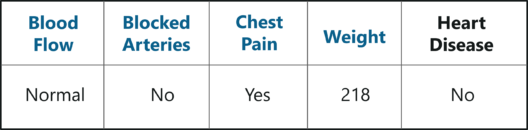 袋外样品 = R 中的随机林
袋外样品 = R 中的随机林
不包括在引导式数据集中的此示例数据集称为袋外 (OOB) 数据集。袋外数据集用于检查模型的准确性,因为模型不是使用此 OOB 数据创建的,它将使我们很好地了解模型是否有效。
在我们的例子中,OOB 数据集的输出类为”否”。因此,为了使我们的随机林模型准确无误,如果我们在决策树下运行 OOB 数据,我们必须获得大多数”否”的投票。这个过程是对所有OOB样品进行的,在我们的例子中,我们只有一个OOB,但是,在大多数问题中,通常有更多的样本。
因此,最终,我们可以根据正确分类的OOB样本的比例来测量随机林的准确性。
分类错误的 OOB 样本的比例称为袋外错误。因此,这是随机林的工作原理示例。
现在,让我们把手弄脏,实现随机林算法来解决更复杂的问题。
随机林在R中的实际实现
甚至住在岩石下的人也会听说过一部叫泰坦尼克号的电影。但是你们中有多少人知道这部电影是基于一个真实事件?卡格尔收集了一个数据集,其中包含谁幸存下来,谁在泰坦尼克号上死亡的数据。
问题陈述:建立一个随机森林模型,可以研究泰坦尼克号上一个人的特征,并预测他们存活的可能性。
数据集描述:数据集中针对每个人有几个变量/要素:
- 舱位:乘客舱位(第1、2或3)
- 性
- 年龄
- sibsp:兄弟姐妹/配偶船上人数
- 羊皮纸:父母/子女登机人数
- 票价:乘客支付的费用
- 开始:在那里他们得到了船上(C = 瑟堡;Q = 皇后镇;S = 南安普敦)
我们将使用 RStudio 在 R 中运行以下代码段,因此请继续打开 RStudio。对于此演示,您需要安装护理包和随机森林包。
install.packages("caret", dependencies = TRUE)
install.packages("randomForest")下一步是将包加载到工作环境中。
library(caret)
library(randomForest)是时候加载数据了;我们将使用 read.table 函数来执行此操作csv 和 test.csv)
train <- read.table('C:/Users/zulaikha/Desktop/titanic/train.csv', sep=",", header= TRUE)上述命令在文件”train.csv”中读取,使用分隔符”,(显示该文件是 CSV 文件),包括标题行作为列名称,并将其分配给 R 对象训练。
现在,让我们在测试数据中阅读:
test <- read.table('C:/Users/zulaikha/Desktop/titanic/test.csv', sep = ",", header = TRUE为了比较训练和测试数据,让我们看一下训练集的前几行:
head(train)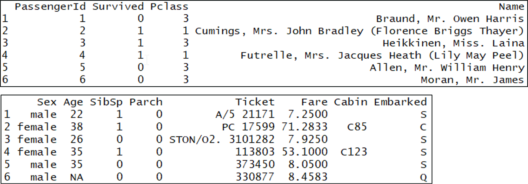
您会注意到,每行都有一列”生存”,如果保存此值的人高于 0.5,并且没有低于 0.5,则该列的概率介于 0 和 1 之间。现在,让我们将训练集与测试集进行比较:
head(test)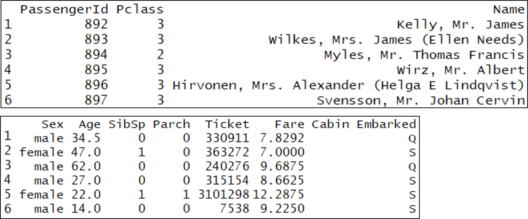 训练集和测试集之间的主要区别是训练集已标记,但测试集未标记。火车组显然没有一个叫做”生存”的列,因为我们必须预测,对于每个登上泰坦尼克号的人。
训练集和测试集之间的主要区别是训练集已标记,但测试集未标记。火车组显然没有一个叫做”生存”的列,因为我们必须预测,对于每个登上泰坦尼克号的人。
在我们更进一步之前,构建模型时最重要的因素是选择在模型中使用的最佳功能。它从来不是选择最好的算法或使用最复杂的R包。现在,”功能”只是一个变量。
因此,这让我们想到一个问题,我们如何选择最重要的变量使用?简单的方法是使用交叉选项卡和条件框图。
交叉选项卡以可以理解的方式表示两个变量之间的关系。根据我们的问题,我们想知道哪些变量是”生存”的最佳预测变量。让我们来看看”生存”和相互变量之间的交叉选项卡。在 R 中,我们使用表函数:
table(train[,c('Survived', 'Pclass')])
Pclass
Survived 1 2 3
0 80 97 372
1 136 87 119从横表中,我们可以看到”Pclass”可能是”生存”的有用预测变量。这是因为横表的第一栏显示,在1级的乘客中,有136人幸存,80人死亡(即63%的头等舱乘客幸存下来)。另一方面,在2级,87人幸存,97人死亡(即只有47%的二等舱乘客幸存下来)。最后,在3级,119人幸存,372人死亡(即只有24%的三等乘客幸存下来)。这意味着乘客阶层与生存机会之间有明显的关系。
现在我们知道,我们必须在我们的模型中使用 Pclass,因为它肯定具有一个强大的预测值,即是否有人幸存下来。现在,您可以对数据集中的其他分类变量重复此过程,并决定要包括哪些变量
为了简化操作,让我们使用”条件”框图来比较每个连续变量的分布情况,但条件是乘客是否幸存。但首先,我们需要安装”字段”包:
installxy(火车$生存,火车$年龄)
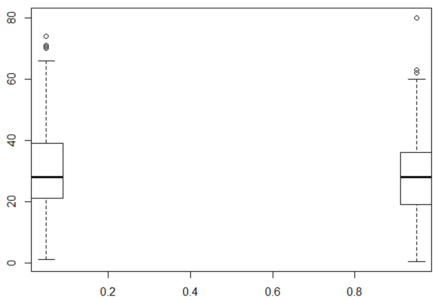 框图 = R 中的随机林
框图 = R 中的随机林幸存下来的人和没有活下来的人的年龄的框图几乎一样。这意味着一个人的年龄对一个人是否存活没有产生很大影响。y 轴为”年龄”,x 轴为”存活”。
此外,如果你总结它,有很多的NA的。因此,让我们排除变量年龄,因为它对生存没有太大的影响,因为 NA 使得它很难使用。
summary(train$Age)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
0.42 20.12 28.00 29.70 38.00 80.00 在下面的箱形图中,对于幸存下来的人和那些没有幸存下来的人,票价的箱线图有很大的不同。同样,y 轴为”票价”,x 轴为”幸存”。
bplot.xy(train$Survived, train$Fare)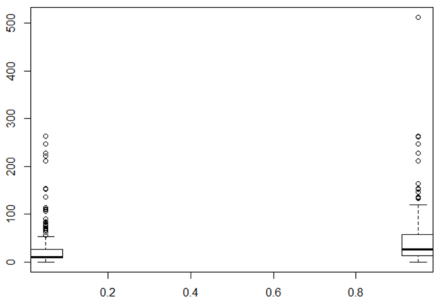 总结,你会发现没有NA的票价。因此,让我们包括这个变量。
总结,你会发现没有NA的票价。因此,让我们包括这个变量。
summary(train$Fare)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00 7.91 14.45 32.20 31.00 下一步是将”生存”转换为因子数据类型,以便 caret 生成分类而不是回归模型。之后,我们使用一个简单的训练命令来训练模型。
现在,我们使用前面讨论的随机林算法对模型进行了训练。随机林非常适合此类问题,因为它执行大量计算并高精度预测结果。
train$Survived <- factor(train$Survived)
# Set a random seed
set.seed(51)
# Training using ‘random forest’ algorithm
model <- train(Survived ~ Pclass + Sex + SibSp +
Embarked + Parch + Fare, # Survived is a function of the variables we decided to include
data = train, # Use the train data frame as the training data
method = 'rf',# Use the 'random forest' algorithm
trControl = trainControl(method = 'cv', # Use cross-validation
number = 5) # Use 5 folds for cross-validation为了评估我们的模型,我们将使用交叉验证分数。
交叉验证用于使用训练数据评估模型的效率。首先,您将训练数据随机划分为 5 个大小相等的部分,称为”折叠”。接下来,根据数据的 4/5 对模型进行训练,并检查其准确性,以您遗漏的 1/5 的数据。然后,对数据的每个拆分重复此过程。
最后,您可以对数据五个不同拆分的百分比精度进行平均,以获得平均精度。Caret 会为您执行此工作,您可以通过查看模型输出来查看分数:
model
Random Forest
891 samples
6 predictor
2 classes: '0', '1'
No pre-processing
Resampling: Cross-Validated (5 fold)
Summary of sample sizes: 712, 713, 713, 712, 714
Resampling results across tuning parameters:
mtry Accuracy Kappa
2 0.8047116 0.5640887
5 0.8070094 0.5818153
8 0.8002236 0.5704306
Accuracy was used to select the optimal model using the largest value.
The final value used for the model was mtry = 5.需要注意的第一件事是,它说,”用于模型的最终值是 mtry = 5。”mtry”是随机林模型的超参数,用于确定模型用于拆分树的变量数。
该表显示了不同的 mtry 值及其在交叉验证下的相应平均精度。Caret 会自动选取在交叉验证下最准确的超参数”mtry”的值。
在输出中,使用 mtry = 5 时,平均精度为 0
在预测测试数据的输出之前,让我们检查一下我们用于预测的变量中是否有任何缺失的数据。如果 Caret 发现任何缺失值,则根本不返回预测。因此,在前进之前,我们必须找到缺失的数据:
summary(test)请注意,变量”Fare”具有一个 NA 值。让我们用”Fare”列的平均值来填充该值。我们使用 if-else 语句来执行此操作。
因此,如果列”Fare”中的条目为 NA,则将其替换为列的平均值,并在采用均值时删除 NA:
test$Fare <- ifelse(is.na(test$Fare), mean(test$Fare, na.rm = TRUE), test$Fare)现在,我们的最后一步是对测试集进行预测。为此,只需调用所训练的模型对象的预测方法。让我们对测试集进行预测,并将其添加为新列。
test$Survived <- predict(model, newdata = test)
test$Survived
在这里,您可以看到每位乘客的”幸存”值(0 或 1)。一个代表生存,0代表死亡。此预测基于”pclass”和”Fare”变量。您也可以使用其他变量,如果它们与登上泰坦尼克号的人是否会生存有某种关系。
我希望你们都发现这个博客信息。如果您有任何想法要分享,请发表评论。
